
(本小题共12分)已知向量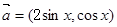 ,
,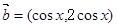 ,函数
,函数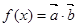 .
.
(Ⅰ)求函数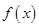 的最小正周期和最大值;
的最小正周期和最大值;
(Ⅱ)求函数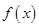 在区间
在区间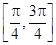 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ)最小正周期是 ;最大值是
;最大值是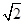 +1(Ⅱ)最大值是2,最小值是1
+1(Ⅱ)最大值是2,最小值是1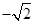
解析试题分析:(Ⅰ)因为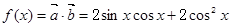 , …1分
, …1分
所以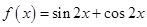 +1 …2分
+1 …2分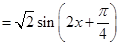 +1. …3分
+1. …3分
所以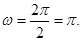 …4分
…4分
又因为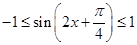 ,
,
所以1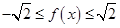 +1. …5分
+1. …5分
所以函数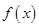 的最小正周期是
的最小正周期是 ;最大值是
;最大值是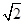 +1. …6分
+1. …6分
(Ⅱ)由(Ⅰ)知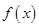
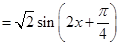 +1.
+1.
因为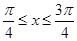 ,所以
,所以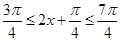 . …7分
. …7分
所以当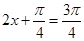 ,即
,即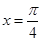 时,函数
时,函数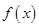 有最大值是2; …9分
有最大值是2; …9分
当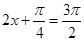 ,即
,即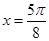 时,函数
时,函数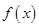 有最小值是1
有最小值是1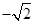 . …11分
. …11分
所以函数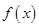 在区间
在区间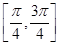 上的最大值是2,最小值是1
上的最大值是2,最小值是1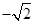 . …12分
. …12分
考点:本小题以向量为载体,考查三角函数的图象和性质,考查学生对三角函数公式的掌握和对三角函数图象的理解和应用.
点评:平面向量与三角的综合性问题大多是以三角题型为背景的一种向量描述.它需要根据向量运算性质将向量问题转化为三角的相关知识来解答,三角知识是考查的主体.考查的要求并不高,解题时要综合利用平面向量的几何意义等将题中的条件翻译成简单的数学问题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
(本题满分13分)已知函数f(x)=cos(- )+cos(
)+cos( ),k∈Z,x∈R.
),k∈Z,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,π)上的减区间;
(3)若f(α)= ,α∈(0,
,α∈(0, ),求tan(2α+
),求tan(2α+ )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
函数 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点, 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形。
为正三角形。
(Ⅰ)求 的值及函数
的值及函数 的值域;
的值域;
(Ⅱ)若 ,且
,且 ,求
,求 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
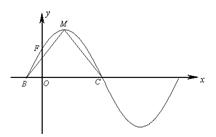
(本小题满分13分)函数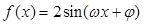
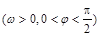 的部分图象如下图所示,该图象与
的部分图象如下图所示,该图象与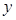 轴交于点
轴交于点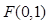 ,与
,与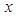 轴交于点
轴交于点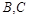 ,
, 为最高点,且
为最高点,且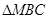 的面积为
的面积为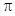 .
.
(Ⅰ)求函数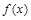 的解析式;
的解析式;
(Ⅱ)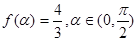 ,求
,求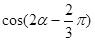 的值.
的值.
(Ⅲ)将函数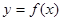 的图象的所有点的横坐标缩短到原来的
的图象的所有点的横坐标缩短到原来的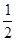 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移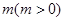 个单位,得函数
个单位,得函数 的图象,若函数
的图象,若函数 为奇函数,求
为奇函数,求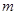 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)已知函数 (其中
(其中 的最小正周期为
的最小正周期为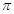 .
.
(Ⅰ)求 的值,并求函数
的值,并求函数 的单调递减区间;
的单调递减区间;
(Ⅱ)在锐角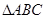 中,
中, 分别是角
分别是角 的对边,若
的对边,若
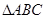 的面积为
的面积为 ,求
,求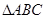 的外接圆面积.
的外接圆面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com