
分析 (1)分类讨论,求出函数的最小值,即可求a;
(2)由柯西不等式:(a2+b2+c2)(d2+e2+f2)≥(ad+be+cf)2,即可求p2+q2+r2的最小值.
解答 解:(1)x≤-2时,f(x)=-$\frac{3}{2}$x-1≥2;
-2<x<0时,f(x)=-$\frac{1}{2}$x+1∈(1,2);
x≥0时,f(x)=$\frac{3}{2}$x+1≥1
∴f(x)的最小值为1,即a=1;
(2)由(1)知,p+q+r=3,又p,q,r为正实数,
∴由柯西不等式得,(p2+q2+r2)(12+12+12)≥(p×1+q×1+r×1)2
=(p+q+r)2=32=9,
即p2+q2+r2≥3,∴p2+q2+r2的最小值为3.
点评 本题主要考查绝对值不等式、柯西不等式等基础知识,考查运算求解能力,考查化归与转化思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{512}$ | B. | -$\frac{341}{512}$ | C. | $\frac{1}{1024}$ | D. | $\frac{1}{2048}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 1.5 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-|x-1| | B. | y=x2-2x+4 | C. | y=ln(x+2) | D. | y=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 简单随机抽样 | B. | 系统抽样 | C. | 分层抽样 | D. | 抽签法 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
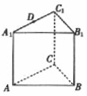 如图所示,已知三棱柱ABC-A1B1C1的所有棱长都相等,AA1⊥平面ABC,D是A1C1的中点,则直线AD与平面B1DC所成的角θ的正弦值为$\frac{4}{5}$.
如图所示,已知三棱柱ABC-A1B1C1的所有棱长都相等,AA1⊥平面ABC,D是A1C1的中点,则直线AD与平面B1DC所成的角θ的正弦值为$\frac{4}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com