
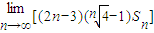 = .
= .
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
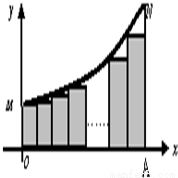
 (2009•长宁区二模)如图,曲线C:y=2x(0≤x≤2)两端分别为M、N,且NA⊥x轴于点A.把线段OA分成n等份,以每一段为边作矩形,使与x轴平行的边一个端点在曲线C上,另一端点在曲线C的下方,设这n个矩形的面积之和为Sn,则
(2009•长宁区二模)如图,曲线C:y=2x(0≤x≤2)两端分别为M、N,且NA⊥x轴于点A.把线段OA分成n等份,以每一段为边作矩形,使与x轴平行的边一个端点在曲线C上,另一端点在曲线C的下方,设这n个矩形的面积之和为Sn,则| lim |
| n→∞ |
| n | 4 |
查看答案和解析>>
科目:高中数学 来源:2011-2012年江西省南昌二中高三(上)第四次月考数学试卷(文科)(解析版) 题型:选择题
 ),则( )
),则( )

 ,φ=
,φ=
 或ω=
或ω= ,φ=
,φ=
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若x1=-1,x2=2,求函数f(x)的解析式;
(2)若|x1|+|x2|=![]() ,求b的最大值;
,求b的最大值;
(3)若x1<x<x2,且x2=a,函数g(x)=f′(x)-a(x-x1),求证:|g(x)|≤![]() a(3a+2)2.
a(3a+2)2.
(文)如图,N为圆x2+(y-2)2=4上的点,OM为直径,连结MN并延长交x轴于点C,过C引直线垂直于x轴,且与弦ON的延长线交于点D.

(1)已知点N(![]() ,1),求点D的坐标;
,1),求点D的坐标;
(2)若点N沿着圆周运动,求点D的轨迹E的方程;
(3)设P(0,a)(a>0),Q是点P关于原点的对称点,直线l过点P交曲线E于A、B两点,点H在射线QB上,且AH⊥PQ,求证:不论l绕点P怎样转动,恒有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com