
��ƽ��ֱ������ϵ�ϣ��費��ʽ��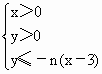 (n��N*)����ʾ��ƽ������ΪDn����Dn�ڵ�����(����������������Ϊ�����ĵ�)�ĸ���Ϊan(n��N*)��
(n��N*)����ʾ��ƽ������ΪDn����Dn�ڵ�����(����������������Ϊ�����ĵ�)�ĸ���Ϊan(n��N*)��
(1)��a1��a2��a3������an�ı���ʽ(����֤��)
(2)������{an}��ǰ���ΪSn������![]() ��ǰ���Tn����ʹ����ʽTn��an��
��ǰ���Tn����ʹ����ʽTn��an��![]() ��һ��n��N*�����������������k��ֵ��
��һ��n��N*�����������������k��ֵ��
(3)��n��N*��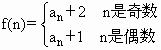 ���Ƿ����m��N*��ʹf(m��15)��5f(m)�����������ڣ����m��ֵ���������ڣ���˵�����ɣ�
���Ƿ����m��N*��ʹf(m��15)��5f(m)�����������ڣ����m��ֵ���������ڣ���˵�����ɣ�
|
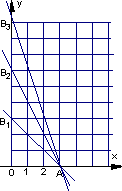
�����⣺ ����(1)��n��1ʱ��D1ΪRt��OAB1���ڲ�����б�ߣ���ʱ ������n��2ʱ��D2ΪRt��OAB2���ڲ�����б�ߣ� ������ʱa2=6��2�� ������n��3ʱ��D3ΪRt��OAB3���ڲ�����б�ߣ� ������ʱa3=9��3�� �����ɴ˿ɲ���an��3n��4�� ����(2)��an��3n��������{an}������Ϊ3������Ϊ3�ĵȲ����У� ������ ���� ���� ������ �������� ���� ������ ���� ����(3) ������ ������ ������� ������ ������ ������� ��������
|



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
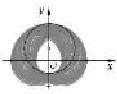 ��ͼ����Ӱ�Ǽ���P={��x��y��|��x-cos�ȣ�2+��y-sin�ȣ�2=4��0�ܦȡܦ�}��ƽ��ֱ������ϵ�ϱ�ʾ�ĵ㼯������Ӱ�м����硰ˮ�Ρ����ֵ�������ڣ�������
��ͼ����Ӱ�Ǽ���P={��x��y��|��x-cos�ȣ�2+��y-sin�ȣ�2=4��0�ܦȡܦ�}��ƽ��ֱ������ϵ�ϱ�ʾ�ĵ㼯������Ӱ�м����硰ˮ�Ρ����ֵ�������ڣ�������A����+
| ||||
B��
| ||||
C��
| ||||
| D����+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
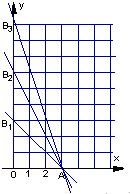 ��ƽ��ֱ������ϵ�ϣ��費��ʽ��
��ƽ��ֱ������ϵ�ϣ��費��ʽ��
|
| 1 |
| Sn |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| 1 |
| anan+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com