
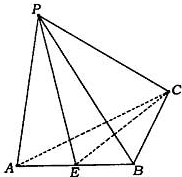
 如图已知四面体P-ABC中,AB=BC=1,AC=
如图已知四面体P-ABC中,AB=BC=1,AC=| 2 |
| 3 |
| π |
| 4 |
| π |
| 4 |
| 2 |
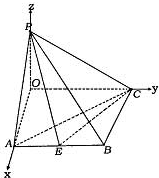 解:(1)由AB=BC=1,AC=
解:(1)由AB=BC=1,AC=| 2 |
| 3 |
| π |
| 4 |
| 2 |
| OC•CF |
| OF |
| ||
| 5 |
2
| ||
| 5 |
| OP |
| OG |
| ||||
|
| ||
| 2 |
| ||
| 2 |
| OP•OG |
| PG |
| ||||||
|
2
| ||
| 7 |
| ||
| 7 |


科目:高中数学 来源: 题型:
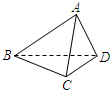 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.查看答案和解析>>
科目:高中数学 来源:四川省南充高中2008-2009学年高二下学期第四次月考数学文 题型:044
如图,已知PA垂直于⊙O所在平面,AB是⊙O的直径,点C为圆周上异于A、B的一点.

(1)若一个n面体中有m个面是直角三角形,则称这个n面体的直度为![]() .那么四面体P-ABC的直度为多少?说明理由;
.那么四面体P-ABC的直度为多少?说明理由;
(2)如图,若四面体P-ABC中,AP=AB=1,AE⊥PB,垂足为E,AF⊥PC,垂足为F.设∠EAF=![]() ,
,![]() 为△AEF面积的函数,求
为△AEF面积的函数,求![]() 取最大值时二面角A-PB-C的大小.
取最大值时二面角A-PB-C的大小.

查看答案和解析>>
科目:高中数学 来源:2011年江苏省南京师大附中高考数学四模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年江苏省高考数学权威预测试卷(1)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年江苏省南通市通州高级中学高考综合测试数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com