解:(1)∵抛物线y
2=8x的焦点坐标为F(2,0)
∴椭圆
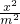
+
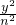
=1(m>0,n>0)的右焦点为F(2,0),可得m
2-n
2=4…①
∵椭圆的离心率e=

=

,∴
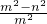
=

…②
联解①②,得m
2=16,n
2=12
∴该椭圆的标准方程为

+
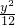
=1;
(2)∵椭圆
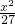
+
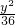
=1经过点A的纵坐标为4
∴设A(t,4),可得
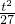
+
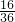
=1,解之得t=
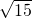
,A(
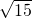
,4)
∵椭圆
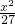
+
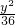
=1的焦点为(0,±3),双曲线与椭圆
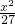
+
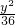
=1有相同的焦点,
∴双曲线的焦点为(0,±3),因此设双曲线方程为
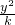
-
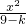
=1(0<k<9)
将点A(
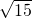
,4)代入,得
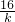
-
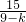
=1,解之得k=4(舍负)
∴双曲线方程为
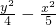
=1
分析:(1)由抛物线方程得到它的焦点坐标为F(2,0)也是椭圆的右焦点,由此得到m
2-n
2=4.根据椭圆离心率为

,得到m
2-n
2=

m
2,联解得到m
2=16,n
2=12,即得该椭圆的标准方程;
(2)根据椭圆
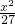
+
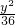
=1经过点A的纵坐标为4,算出A的横坐标是
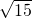
,得A(
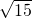
,4).算出椭圆的焦点坐标为(0,±3)也是双曲线的焦点,由此可设双曲线方程为
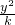
-
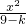
=1(0<k<9),代入点A坐标解出k=4,从而得到此双曲线的标准方程.
点评:本题给出两个曲线有公共的焦点,在已知它们一个交点坐标的情况下求曲线的方程,着重考查了椭圆、双曲线和抛物线的标准方程和简单几何性质等知识,属于基础题.

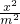 +
+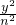 =1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为 ,求椭圆的标准方程.
,求椭圆的标准方程.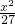 +
+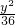 =1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程.
=1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程.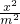 +
+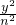 =1(m>0,n>0)的右焦点为F(2,0),可得m2-n2=4…①
=1(m>0,n>0)的右焦点为F(2,0),可得m2-n2=4…① =
= ,∴
,∴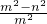 =
= …②
…② +
+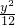 =1;
=1;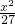 +
+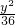 =1经过点A的纵坐标为4
=1经过点A的纵坐标为4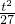 +
+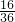 =1,解之得t=
=1,解之得t=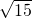 ,A(
,A(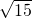 ,4)
,4)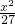 +
+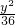 =1的焦点为(0,±3),双曲线与椭圆
=1的焦点为(0,±3),双曲线与椭圆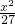 +
+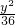 =1有相同的焦点,
=1有相同的焦点,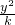 -
-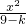 =1(0<k<9)
=1(0<k<9)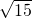 ,4)代入,得
,4)代入,得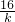 -
-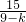 =1,解之得k=4(舍负)
=1,解之得k=4(舍负)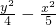 =1
=1 ,得到m2-n2=
,得到m2-n2= m2,联解得到m2=16,n2=12,即得该椭圆的标准方程;
m2,联解得到m2=16,n2=12,即得该椭圆的标准方程;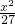 +
+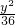 =1经过点A的纵坐标为4,算出A的横坐标是
=1经过点A的纵坐标为4,算出A的横坐标是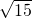 ,得A(
,得A(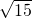 ,4).算出椭圆的焦点坐标为(0,±3)也是双曲线的焦点,由此可设双曲线方程为
,4).算出椭圆的焦点坐标为(0,±3)也是双曲线的焦点,由此可设双曲线方程为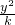 -
-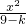 =1(0<k<9),代入点A坐标解出k=4,从而得到此双曲线的标准方程.
=1(0<k<9),代入点A坐标解出k=4,从而得到此双曲线的标准方程.

 已知椭圆C:
已知椭圆C:![]() 和圆
和圆![]() ,且圆C与x轴交于A1,A2两点 (1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。 (2)设点
,且圆C与x轴交于A1,A2两点 (1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。 (2)设点![]() 在直线
在直线![]() 上,若存在点
上,若存在点![]() ,使得
,使得![]() (O为坐标原点),求
(O为坐标原点),求![]() 的取值范围。
的取值范围。 +
+ =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 .
. ·
· +
+ ·
· =8,求k的值.
=8,求k的值.