
科目:高中数学 来源:不详 题型:填空题
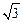 ,∠PAB=300,则线段PB的长为 ..
,∠PAB=300,则线段PB的长为 ..查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 如图1:等边
如图1:等边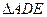 可以看作由等边
可以看作由等边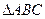 绕顶点
绕顶点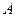 经过旋转相似变换得到.但是我们注意到图形中的
经过旋转相似变换得到.但是我们注意到图形中的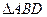 和
和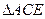 的关系,上述变换也可以理解为图形是由
的关系,上述变换也可以理解为图形是由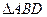 绕顶点
绕顶点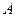 旋转
旋转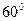 形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转
形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转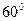 形成的.
形成的.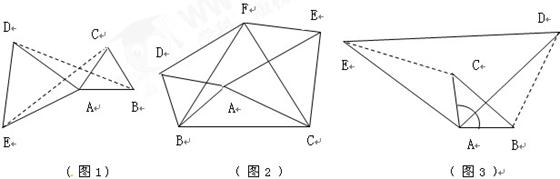
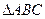 中,
中,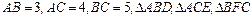 都是等边三角形,求四边形
都是等边三角形,求四边形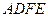 的面积;
的面积;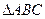 ∽
∽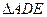 ,
,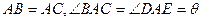 ,仿照上述结论,推广出符合图3的结论.(写出结论即可)
,仿照上述结论,推广出符合图3的结论.(写出结论即可)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

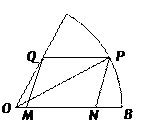
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com