
| A. | l?α | B. | l⊥α | C. | l∥α | D. | l与α斜交 |
分析 由已知可得:$\overrightarrow{n}=-\overrightarrow{a}$,因此$\overrightarrow{n}∥\overrightarrow{a}$,再利用线面垂直的判定即可得出.
解答 解:∵直线l的方向向量为$\overrightarrow{a}$=(1,0,2),平面α的法向量$\overrightarrow{n}$=(-1,0,-2),$\overrightarrow{n}=-\overrightarrow{a}$,
∴$\overrightarrow{n}∥\overrightarrow{a}$,
∴l⊥α.
故选:B.
点评 本题考查了向量共线定理、线面垂直的判定定理,考查了推理能力与计算能力,属于中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
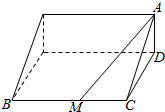 如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.
如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com