
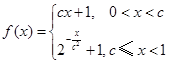 ,满足
,满足 .
. 的不等式
的不等式 .
. 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
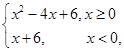 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )| A.(-3,1)∪(3,+∞) | B.(-3,1)∪(2,+∞) |
| C.(-1,1)∪(3,+∞) | D.(-∞,-3)∪(1,3) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.ex+1 | B.ex-1 |
| C.e-x+1 | D.e-x-1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的实根个数分别为a,b,则a+b=
的实根个数分别为a,b,则a+b=
| A.18 | B.21 | C.24 | D.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,Q=
,Q= t,今该公司将5亿元投资于这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).求:
t,今该公司将5亿元投资于这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com