
如图,菱形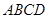 的边长为
的边长为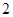 ,
,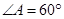 ,
,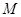 为
为 的中点,则
的中点,则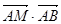 的值为 .
的值为 .
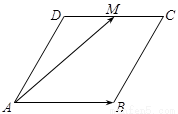
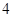
【解析】
试题分析:根据题意,由于菱形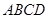 的边长为
的边长为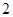 ,
,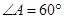 ,
,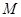 为
为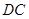 的中点,先以点A位坐标原点建立的直角坐标系,求出其它各点的坐标,然后利用点的坐标表示出
的中点,先以点A位坐标原点建立的直角坐标系,求出其它各点的坐标,然后利用点的坐标表示出
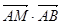
,把所求问题转化为在平面区域内求线性目标函数的最值问题求解即可。解::以点A位坐标原点建立如图所示的直角坐标系,由于菱形ABCD的边长为2,∠A=60°,M为DC的中点,故点A(0,0),则B(2,0),C(3,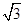 ),D(1,
),D(1,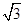 ),M(2,
),M(2,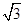 )
)
设N(x,y),N为平行四边形内(包括边界)一动点,对应的平面区域即为平行四边形ABCD及其内部区域.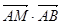 =4,故可知答案为4.
=4,故可知答案为4.
考点:向量在几何中的应用
点评:本题主要考查向量在几何中的应用以及数形结合思想的应用和转化思想的应用,是对基础知识和基本思想的考查,属于中档


科目:高中数学 来源:2011届山东省潍坊市三县高三最后一次模拟考试文数 题型:解答题
(本小题满分12分)
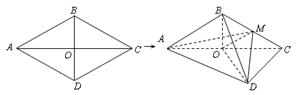
如图,菱形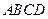 的边长为
的边长为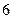 ,
,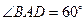 ,
, .将菱形
.将菱形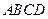 沿对角线
沿对角线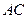 折起,得到三棱锥
折起,得到三棱锥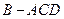 ,点
,点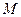 是棱
是棱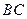 的中点,
的中点,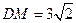 .
.
(Ⅰ)求证: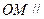 平面
平面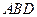 ;
;
(Ⅱ)求证:平面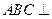 平面
平面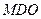 ;
;
(III)求三棱锥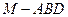 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2014届广东省广州市越秀区高三上学期摸底考试文科数学试卷(解析版) 题型:解答题
如图,菱形 的边长为4,
的边长为4,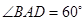 ,
, .将菱形
.将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点,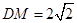 .
.

(1)求证: 平面
平面 ;
;
(2)求证:平面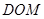
 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三12月月考文科数学 题型:解答题
(本小题满分12分)
如图,菱形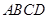 的边长为
的边长为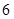 ,
,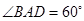 ,
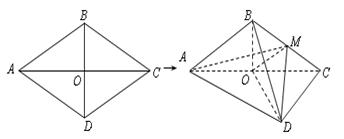
,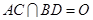 .将菱形
.将菱形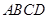 沿对角线
沿对角线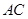 折起,得到三棱锥
折起,得到三棱锥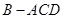 ,点
,点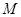 是棱
是棱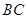 的中点,
的中点,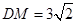 .
.
(1)求证: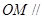 平面
平面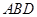 ;
;
(2)求证: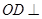 平面
平面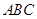 ;平面
;平面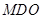
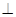 平面
平面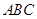 ;
;
(3)求三棱锥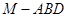 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市西城区高三二模试卷数学(文科) 题型:解答题
如图,菱形 的边长为
的边长为 ,
, ,
, .将菱形
.将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求三棱锥 的体积
的体积

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com