
 )n的展开式中所有二项式系数的和为512,则展开式中x3项的系数为 ________
)n的展开式中所有二项式系数的和为512,则展开式中x3项的系数为 ________ )n的展开式中二项式系数的和为512,求展开式中x3项的系数.因为由二项式性质可直接得到二项式系数和为2n,故可求出n的值,再列出二项式的通项,求出x3项为第几项,代入通项求出系数即可得到答案.
)n的展开式中二项式系数的和为512,求展开式中x3项的系数.因为由二项式性质可直接得到二项式系数和为2n,故可求出n的值,再列出二项式的通项,求出x3项为第几项,代入通项求出系数即可得到答案. )n的展开式中所有二项式系数和为2n
)n的展开式中所有二项式系数和为2n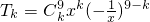 =(-1)9-kC9kx2k-9
=(-1)9-kC9kx2k-9

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com