分析:(1)根据f(x)=(x-3)
3+x-1,可得f(x)-2=(x-3)
3+x-3,构造函数g(x)=f(x)-2,从而g(x)关于(3,0)对称,利用f(a
1)+f(a
2)+…+f(a
7)=14,可得g(a
1)+g(a
2)+…+g(a
7)=0,从而g(a
4)为g(x)与x轴的交点,由此可求a
1+a
2+…+a
7的值.
(2)由sin
>0,sin
>0,…,sin
>0,sin
=0,sin
<0,…,sin
<0,sin
=0,可得到S
1>0,…S
13>0,而S
14=0,从而可得到周期性的规律,从而得到答案.
解答:解:(1)解:∵f(x)=(x-3)
3+x-1,∴f(x)-2=(x-3)
3+x-3,
令g(x)=f(x)-2,
∴g(x)关于(3,0)对称,
∵f(a
1)+f(a
2)+…+f(a
7)=14,
∴f(a
1)-2+f(a
2)-2+…+f(a
7)-2=0
∴g(a
1)+g(a
2)+…+g(a
7)=0,
∴g(a
4)为g(x)与x轴的交点,
因为g(x)关于(3,0)对称,所以a
4=3,
∴a
1+a
2+…+a
7=7a
4=21,
故答案为:21.
(2)解:∵sin
>0,sin
>0,…,sin
>0,sin
=0,sin
<0,…,sin
<0,sin
=0,
∴S
1=sin
>0,
S
2=sin
+sin
>0,…,
S
8=sin
+sin
+…+sin
+sin
+sin
=sin
+…+sin
+sin
>0,
…,
S
12>0,
而S
13=sin
+sin
+…+sin
+sin
+sin
+sin
+…+sin
=0,
S
14=S
13+sin
=0+0=0,
又S
15=S
14+sin
=0+sin
=S
1>0,S
16=S
2>0,…S
27=S
13=0,S
28=S
14=0,
∴S
14n-1=0,S
14n=0(n∈N*),在1,2,…100中,能被14整除的共7项,
∴在S
1,S
2,…,S
100中,为0的项共有14项,其余项都为正数.
故在S
1,S
2,…,S
100中,正数的个数是86.
故答案为:86.
点评:题考查数列与函数的综合,数列与三角函数的综合,考查函数的对称性,考查数列的性质,考查学生分析问题解决问题的能力.



 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案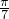 +sin
+sin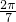 +…+sin
+…+sin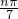 (n∈N+),则在S1,S2,…S100中,正数的个数是________.
(n∈N+),则在S1,S2,…S100中,正数的个数是________.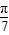 +sin
+sin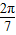 +…+sin
+…+sin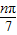 (n∈N+),则在S1,S2,…S100中,正数的个数是______.
(n∈N+),则在S1,S2,…S100中,正数的个数是______.