
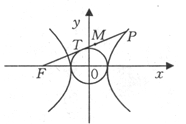
如图,过双曲线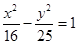 的左焦点F引圆
的左焦点F引圆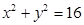 的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|—|MT|=( )
的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|—|MT|=( )
A.1 B.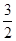 C.
C.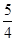 D.2
D.2
 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
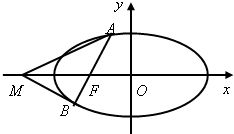 已知离心率为
已知离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年新建二中模拟)如图,过椭圆![]() 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
(1)求椭圆![]() 的“左特征点”M的坐标;
的“左特征点”M的坐标;
(2)试根据(1)中的结论猜测:椭圆![]()
![]() 的“左特征点”M是一个怎样的点?并证明你的结论.
的“左特征点”M是一个怎样的点?并证明你的结论.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图,从双曲线![]() 的左焦点F引圆
的左焦点F引圆![]() 的切线,切点为T.延长FT交双曲线右支于P点若M为线段FP的中点,O为坐标原点,则
的切线,切点为T.延长FT交双曲线右支于P点若M为线段FP的中点,O为坐标原点,则![]() 与
与![]() 的大小关系为 ( )
的大小关系为 ( )
A.![]() B.
B.![]()
C.![]() D.不确定
D.不确定

查看答案和解析>>
科目:高中数学 来源:2011-2012年湖南省衡阳市高二第三次月考考试理科数学 题型:解答题
( 9分) 如图,过椭圆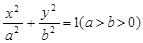 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆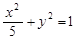 的“左特征点”M的坐标;
的“左特征点”M的坐标;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com