
已知函数 ,函数
,函数 是区间
是区间 上的减函数.
上的减函数.
(1)求 的最大值;
的最大值;
(2)若 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 的根的个数.
的根的个数.
(1)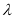 的最大值为
的最大值为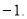 (2)
(2)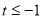 .(3)当
.(3)当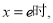
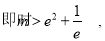 方程无解;
方程无解;
当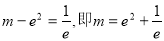 时,方程有一个根;当
时,方程有一个根;当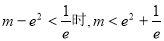 时,方程有两个根.
时,方程有两个根.
【解析】
试题分析:(1)由题意由于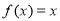 ,所以函数
,所以函数 ,又因为该函数是在区间
,又因为该函数是在区间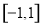 上的减函数,所以可以得到
上的减函数,所以可以得到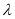 的范围;
的范围;
(2)由对所有满足条件的实数及对任意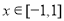 ,
,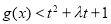 在
在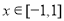 上恒成立
上恒成立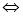
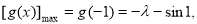 解出即可;
解出即可;
(3)利用方程与函数的关系可以构造成两函数图形的交点个数加以分析求解.
试题解析:(1)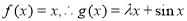 ,
,
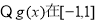 上单调递减,
上单调递减,
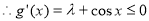
 在[-1,1]上恒成立,
在[-1,1]上恒成立,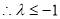 ,故
,故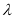 的最大值为
的最大值为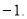
(2)由题意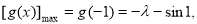
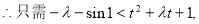
 (其中
(其中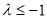 ),恒成立,
),恒成立,
令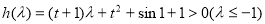 ,
,
若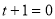 ,则有
,则有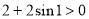 恒成立,
恒成立,
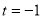
若 ,则
,则 ,
,
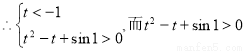 恒成立,
恒成立,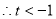
综上,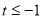
(3)由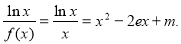
令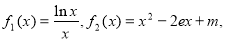
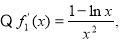
当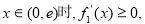
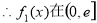 上为增函数;
上为增函数;
当 时,
时,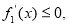
 为减函数;
为减函数;
当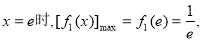 而
而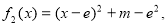
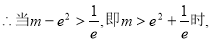 方程无解;
方程无解;
当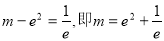 时,方程有一个根;
时,方程有一个根;
当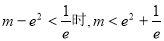 时,方程有两个根.
时,方程有两个根.
考点:导数在最大值、最小值问题中的应用;利用导数研究函数的单调性;利用导数求闭区间上函数的最值.


科目:高中数学 来源:2015届山西省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
9件产品中,有4件一等品,3件二等品,2件三等品,现在要从中抽出4件产品来检查,至少有两件一等品的抽取方法是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二3月月考理科数学试卷(解析版) 题型:选择题
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)> 0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二3月月考文科数学试卷(解析版) 题型:选择题
“渐升数” 是指每个数字比它左边的数字大的正整数(如1458) ,若把四位“渐升数”按从小到大的顺序排列.则第30个数为( )
A.1278 B.1346 C.1359 D.1579
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二3月月考文科数学试卷(解析版) 题型:选择题
在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当
 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的 =20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )
=20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )
A.有95%的把握认为两者有关 B.约有95%的打鼾者患心脏病
C.有99%的把握认为两者有关 D.约有99%的打鼾者患心脏病
查看答案和解析>>
科目:高中数学 来源:2015届山西大学附中高二第二学期月考理科数学试卷(解析版) 题型:填空题
已知函数 ,在定义域
,在定义域 上表示的曲线过原点,且在
上表示的曲线过原点,且在 处的切线斜率均为
处的切线斜率均为 .有以下命题:
.有以下命题:
① 是奇函数;②若
是奇函数;②若 在
在 内递减,则
内递减,则 的最大值为4;③
的最大值为4;③ 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 ; ④若对
; ④若对 ,
, 恒成立,则
恒成立,则 的最大值为2.其中正确命题的序号为
的最大值为2.其中正确命题的序号为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com