
【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的女学生中随机选出100名并统计她们的身高(单位:cm),得到的频数分布表如下:
分组 |
|
|
|
|
频数 | 20 | 20 | 50 | 10 |
(1)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 内的女生应抽取几人?
内的女生应抽取几人?
(2)在(1)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.
科目:高中数学 来源: 题型:
【题目】军训时,甲、乙两名同学进行射击比赛,共比赛10场,每场比赛各射击四次,且用每场击中环数之和作为该场比赛的成绩.数学老师将甲、乙两名同学的10场比赛成绩绘成如图所示的茎叶图,并给出下列4个结论:(1)甲的平均成绩比乙的平均成绩高;(2)甲的成绩的极差是29;(3)乙的成绩的众数是21;(4)乙的成绩的中位数是18.则这4个结论中,正确结论的个数为( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十七世纪法国数学家费马提出猜想:“当整数![]() 时,关于
时,关于![]() 的方程
的方程![]() 没有正整数解”.经历三百多年,于二十世纪九十年中期由英国数学家安德鲁
没有正整数解”.经历三百多年,于二十世纪九十年中期由英国数学家安德鲁![]() 怀尔斯证明了费马猜想,使它终成费马大定理,则下面说法正确的是( )
怀尔斯证明了费马猜想,使它终成费马大定理,则下面说法正确的是( )
A. 存在至少一组正整数组![]() 使方程
使方程![]() 有解
有解
B. 关于![]() 的方程
的方程![]() 有正有理数解
有正有理数解
C. 关于![]() 的方程
的方程![]() 没有正有理数解
没有正有理数解
D. 当整数![]() 时,关于
时,关于![]() 的方程
的方程![]() 没有正实数解
没有正实数解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市收集并整理了该市2019年1月份至10月份各月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.( )
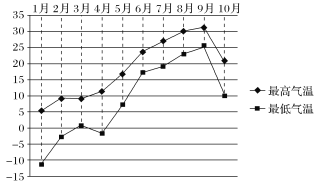
已知该城市各月的最低气温与最高气温具有较好的线性关系,则根据折线图,下列结论正确的是
A.最低气温与最高气温为正相关B.10月的最高气温不低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月D.最低气温低于0 ℃的月份有4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() 是平面
是平面![]() 内的一组基向量,
内的一组基向量,![]() 为
为![]() 内的定点,对于
内的定点,对于![]() 内任意一点
内任意一点![]() ,当
,当![]() 时,则称有序实数对
时,则称有序实数对![]() 为点
为点![]() 的广义坐标,若点
的广义坐标,若点![]() 、
、![]() 的广义坐标分别为
的广义坐标分别为![]() 、
、![]() ,对于下列命题:
,对于下列命题:
① 线段![]() 、
、![]() 的中点的广义坐标为
的中点的广义坐标为![]() ;
;
② A、![]() 两点间的距离为
两点间的距离为![]() ;
;
③ 向量![]() 平行于向量
平行于向量![]() 的充要条件是
的充要条件是![]() ;
;
④ 向量![]() 垂直于向量
垂直于向量![]() 的充要条件是
的充要条件是![]() .
.
其中的真命题是________(请写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定数列![]() ,若数列
,若数列![]() 满足:对任意
满足:对任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“相伴数列”.
的“相伴数列”.
(1)若![]() ,且数列
,且数列![]() 是数列
是数列![]() 的“相伴数列”,试写出
的“相伴数列”,试写出![]() 的一个通项公式,并说明理由;
的一个通项公式,并说明理由;
(2)设![]() ,证明:不存在等差数列
,证明:不存在等差数列![]() ,使得数列
,使得数列![]() 是数列
是数列![]() 的“相伴数列”;
的“相伴数列”;
(3)设![]() ,
,![]() (其中
(其中![]() ),若
),若![]() 是数列
是数列![]() 的“相伴数列”,试分析实数b、q的取值应满足的条件.
的“相伴数列”,试分析实数b、q的取值应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 、
、![]() 、
、![]() 均为正整数,且
均为正整数,且![]() ,
,![]() 为一素数,
为一素数,![]() 、
、![]() 、
、![]() 的
的![]() 进制表示分别为
进制表示分别为![]() ,其中,
,其中,![]() .证明:
.证明:
(1)若![]() ,且对整数
,且对整数![]()
![]() 均有
均有![]() ,则
,则![]() ,其中,
,其中,![]() 表示不超过实数
表示不超过实数![]() 的最大整数.
的最大整数.
(2)![]()
![]() ,其中,
,其中,![]() 表示集合A中元素的个数.
表示集合A中元素的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 为偶函数,求
为偶函数,求![]() 的值并写出
的值并写出![]() 的增区间;
的增区间;
(Ⅱ)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,当
,当![]() 时,求
时,求![]() 的最小值;
的最小值;
(Ⅲ)对任意的![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com