练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】 的单调递减区间为 ．

    【答案】[kπ﹣ ，kπ+ ]（k∈Z）
    【解析】解：令t=sinxcosx+cos2x，则y= 单调递减， t=sinxcosx+cos2x= + sin（2x+ ）＞0，
    令2kπ﹣ ≤2x+ ≤2kπ+
    解得kπ﹣ ≤x≤kπ+ ，单调递增区间为[kπ﹣ ，kπ+ ]（k∈Z），
    ∴ 的单调递减区间为[kπ﹣ ，kπ+ ]（k∈Z），
    所以答案是[kπ﹣ ，kπ+ ]（k∈Z）．
    【考点精析】解答此题的关键在于理解复合函数单调性的判断方法的相关知识，掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x)，y=f(u)的单调性密切相关，其规律：“同增异减”，以及对正弦函数的单调性的理解，了解正弦函数的单调性：在上是增函数；在上是减函数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直线 ，若存在实数 使得一条曲线与直线 由两个不同的交点，且以这两个交点为端点的线段长度恰好等于 ，则称此曲线为直线 的“绝对曲线”.下面给出的四条曲线方程：

    ① ；② ；③ ；④ .

    其中直线 的“绝对曲线”的条数为（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．　

    （Ⅰ）若在定义域与内单调递增，求实数的值；

    （Ⅱ）若的极小值大于0，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】是否存在一个等比数列{an}同时满足下列三个条件：①a1+a6=11且a3a4= ；②an+1＞an（n∈N*）；③至少存在一个m（m∈N*且m＞4），使得 am﹣1 ， am2 ， am+1+ 依次构成等差数列？若存在，求出通项公式；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列中， ，数列满足.

    （1）求证:数列是等差数列，写出的通项公式；

    （2）求数列的通项公式及数列中的最大项与最小项.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题 “存在”，命题：“曲线表示焦点在轴上的椭圆”，命题 “曲线表示双曲线”

    （1）若“且”是真命题，求实数的取值范围；

    （2）若是的必要不充分条件，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若一个四位数的各位数字相加和为，则称该数为“完美四位数”，如数字“”.试问用数字组成的无重复数字且大于的“完美四位数”有（ ）个

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数， （）.

    （1）求函数的单调增区间；

    （2）当时，记，是否存在整数，使得关于的不等式有解？若存在，请求出的最小值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

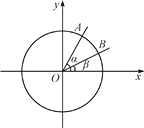
    【题目】如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为， .求：

    （1）tan(α＋β)的值；

    （2）α＋2β的大小．

    查看答案和解析>>

    同步练习册答案