
【题目】已知直线![]() ,若存在实数
,若存在实数![]() 使得一条曲线与直线
使得一条曲线与直线![]() 由两个不同的交点,且以这两个交点为端点的线段长度恰好等于
由两个不同的交点,且以这两个交点为端点的线段长度恰好等于![]() ,则称此曲线为直线
,则称此曲线为直线![]() 的“绝对曲线”.下面给出的四条曲线方程:
的“绝对曲线”.下面给出的四条曲线方程:
①![]() ;②
;② ![]() ;③
;③![]() ;④
;④![]() .
.
其中直线![]() 的“绝对曲线”的条数为( )
的“绝对曲线”的条数为( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】依题意可知,直线![]() 恒过定点
恒过定点![]() .对于①,函数
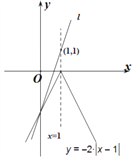
.对于①,函数![]() 的图象关于直线
的图象关于直线![]() 对称,如图所示,所以直线
对称,如图所示,所以直线![]() 与其只能有一个交点,故满足题意的
与其只能有一个交点,故满足题意的![]() 不存在,故① 不符合题意;
不存在,故① 不符合题意;
对于② ,方程![]() 的图象为以点
的图象为以点![]() 为圆心的圆,因此直线
为圆心的圆,因此直线![]() 过圆心,直线与圆两个交点所组成的线段长为
过圆心,直线与圆两个交点所组成的线段长为![]() ,故当
,故当![]() ,直线
,直线![]() 或
或![]() ,直线斜率的绝对值等于截线段长度,即
,直线斜率的绝对值等于截线段长度,即![]() 存在,故② 符合题意;对于③ ,此曲线为一个椭圆,定点
存在,故② 符合题意;对于③ ,此曲线为一个椭圆,定点![]() 在椭圆上,将直线方程代入可得
在椭圆上,将直线方程代入可得![]() ,所以
,所以![]() ,若曲线是直线的“绝对曲线”,则
,若曲线是直线的“绝对曲线”,则![]() ,即
,即![]() ,化简得
,化简得![]() ,令
,令![]() ,则问题转化为存在
,则问题转化为存在![]() ,使得
,使得![]() 成立,因为
成立,因为![]() ,且
,且![]() 为连续函数,所以在区间
为连续函数,所以在区间![]() 存在零点,即
存在零点,即![]() 存在实根,故③符合题意;对于④,首先明确两个极限情况:
存在实根,故③符合题意;对于④,首先明确两个极限情况: ![]() ,此时斜率绝对值无穷大,截线段长度为有限值;
,此时斜率绝对值无穷大,截线段长度为有限值; ![]() ,此时斜率绝对值为零,且当斜率绝对值趋于零时,截线段长度趋于无穷大;若将直线
,此时斜率绝对值为零,且当斜率绝对值趋于零时,截线段长度趋于无穷大;若将直线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,可见斜率绝对值变化趋势为由正无穷单调递减至零,截线段长度变化趋势为从一有限值趋于正无穷(变化过程不一定单调),设
,可见斜率绝对值变化趋势为由正无穷单调递减至零,截线段长度变化趋势为从一有限值趋于正无穷(变化过程不一定单调),设![]() 为斜率绝对值变化情况,
为斜率绝对值变化情况, ![]() 为线段长度变化情况,
为线段长度变化情况, ![]() 为转动角度,做出示意图如下:
为转动角度,做出示意图如下:

必存在某一转动角度![]() 使得
使得![]() 与图象
与图象![]() 相交,即存在
相交,即存在![]() 使得直线斜率的绝对值等于截线段长度,故④符合题意,直线
使得直线斜率的绝对值等于截线段长度,故④符合题意,直线![]() 的“绝对曲线”的条数为4,故选C.
的“绝对曲线”的条数为4,故选C.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏。将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随即从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
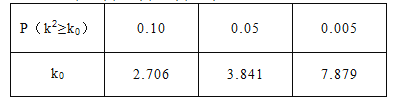
(Ⅰ)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
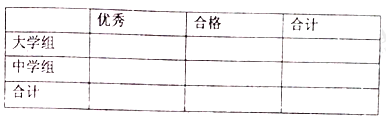
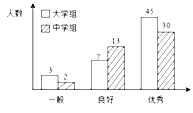
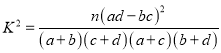 注:其中
注:其中![]() .
.
(Ⅱ)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6,在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为![]() ,在选出的6名良好等级的选手中任取一名,记其编号为
,在选出的6名良好等级的选手中任取一名,记其编号为![]() ,求使得方程组
,求使得方程组![]() 有唯一一组实数解
有唯一一组实数解![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的焦距为
(a>b>0)的焦距为![]() ,且椭圆C过点A(1,
,且椭圆C过点A(1, ![]() ),
),
(Ⅰ)求椭圆C的方程;
(Ⅱ)若O是坐标原点,不经过原点的直线L:y=kx+m与椭圆交于两不同点P(x1,y1),Q(x2,y2),且y1y2=k2x1x2,求直线L的斜率k;
(Ⅲ)在(Ⅱ)的条件下,求△OPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
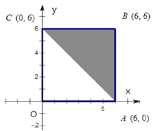
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且满足Sn=2﹣an , n=1,2,3,….
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,且bn+1=bn+an , 求数列{bn}的通项公式;
(3)设cn=n(3﹣bn),求数列{cn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1= ![]() an+t,a1=
an+t,a1= ![]() (t为常数,且t≠
(t为常数,且t≠ ![]() ).
).
(1)证明:{an﹣2t}为等比数列;
(2)当t=﹣ ![]() 时,求数列{an}的前几项和最大?
时,求数列{an}的前几项和最大?
(3)当t=0时,设cn=4an+1,数列{cn}的前n项和为Tn , 若不等式 ![]() ≥2n﹣7对任意的n∈N*恒成立,求实数k的取值范围.
≥2n﹣7对任意的n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(14分)一根直木棍长为6m,现将其锯为2段.
(1)若两段木棍的长度均为正整数,求恰有一段长度为2m的概率;
(2)求锯成的两段木棍的长度均大于2m的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com