练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

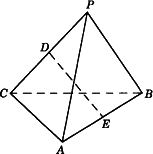
    如下图，P是平面ABC外一点，PA＝4，，D、E分别为PC和AB的中点，且DE＝3．求异面直线PA和BC所成角的大小．

    答案：
    解析：

    解析：取AC中点F，连结DF、EF，在△PAC中，∵D是PC中点，F是AC中点，则DF∥PA，同理可得EF∥BC，∴∠DFE为异面直线PA与BC所成的角．在△DEF中，DE＝3，又DF＝PA＝2，EF＝BC＝，∴，∴∠DFE＝90°，即异面直线PA与BC所成的角为90°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：湖北省黄冈市麻城博达学校2008届高三12月份综合测试数学试卷(文理合卷) 题型：044

    如下图，PCBM是直角梯形，∠PCB＝90°，PM∥BC，PM＝1，BC＝2，又AC＝1，∠ACB＝120°，AB⊥PC，直线AM与直线PC所成的角为60°．

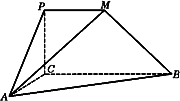
    (Ⅰ)求证：平面PAC⊥平面ABC；

    (Ⅱ)求二面角M－AC－B的大小；

    (Ⅲ)求三棱锥P－MAC的体积．

    查看答案和解析>>

    科目：高中数学 来源：湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型：044

    已知：如下图，P是正方形ABCD所在平面外一点，PA＝PB＝PC＝PD＝a，AB＝a．

    求：平面APB与平面CPD相交所成较大的二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图，在正四棱锥P—ABCD中，PA=AB，E是AB的中点，G是△PCD的重心，则在平面PCD内过G点且与PE垂直的直线有

    A.0条                          B.1条                   C.2条                          D.无数条

    查看答案和解析>>

    科目：高中数学 来源： 题型：

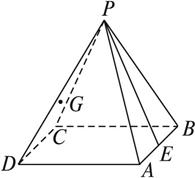
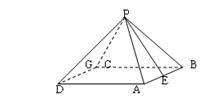
    如下图，在正四棱锥P-ABCD中，PA=AB，E是AB的中点，G是△PCD的重心，则在平面PCD内过G点且与PE垂直的直线有（   ）

    A、0条  B、1条   C、2条    D、无数条

    查看答案和解析>>

    同步练习册答案