【答案】
分析:(1)依题意点P
n的坐标为(x
n,y
n+1),故
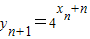
=
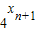
,从而能求出数列{x
n}的通项公式.
(2)由
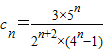
,知
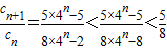
,当n≥2时,
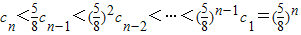
,故T
2n-1=c
1+c
2+…+c
2n-1≤
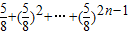
.由此能够证明
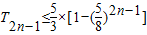
;
(3)由a
n=x
n+1-x
n=n,知

,由
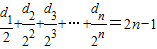
,知
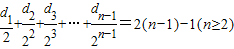
,故
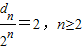
,由此能够比较A
n与
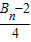
的大小.
解答:解:(1)依题意点P
n的坐标为(x
n,y
n+1),
∴
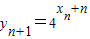
=
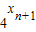
,
∴x
n+1=x
n+n,
∴x
n=x
n-1+n-1=x
n-2+(n-2)+(n-1)=…=x
1+1+2+…+(n-1)=
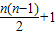
.
(2)∵
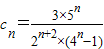
,
∴
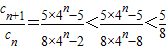
,…(5分)
∴当n≥2时,
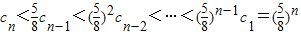
,
∴T
2n-1=c
1+c
2+…+c
2n-1≤
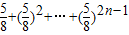
=
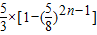
,(当n=1时取“=”).…(8分)
(3)∵a
n=x
n+1-x
n=n,
∴
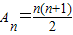
,
由
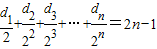
,
知
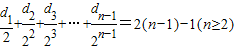
,
∴
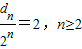
,
而d
1=2,
∴
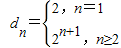
,
于是
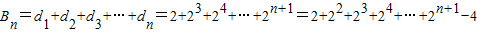
=
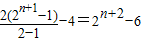
.
∴
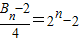
.…(10分)
当n=1,2时
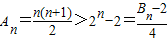
;
当n=3时,
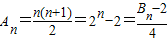
当n≥4时,
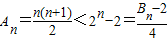
下面证明:当n≥4时,
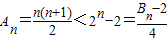
证法一:(利用组合恒等式放缩)
当n≥4时,
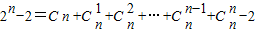
=
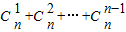
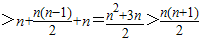
,
∴当n≥4时,

…(13分)
证法二:(函数法)∵n≥4时,
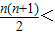
2
n-2
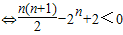
构造函数

,
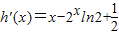
[h'(x)]'=h''(x)=1-2
xln
22
∴当x∈[4,+∞)时,h''(x)=1-2
xln
22<0
∴h'(x)=x-2
xln2在区间[4,+∞)是减函数,
∴当x∈[4,+∞)时,
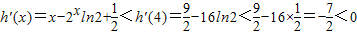
∴
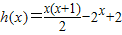
在区间[4,+∞)是减函数,
∴当x∈[4,+∞)时,
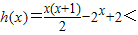
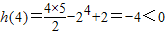
从而n≥4时,

,即
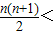
2
n-2,
∴当n≥4时,
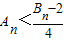
.
点评:本题考查数列的通项公式的求法、不等式的证明和两个表达式大小的比较,具体涉及到数列与不等式的综合运用,放缩法的应用和构造法的应用.

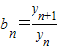 .
.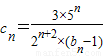 ,数列{cn}的前n项和为Tn,求证:
,数列{cn}的前n项和为Tn,求证: ;
;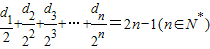 ,记数列{an}的前n项和为An,数列{dn}的前n项和为Bn,试比较An与
,记数列{an}的前n项和为An,数列{dn}的前n项和为Bn,试比较An与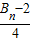 的大小.
的大小.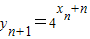 =
=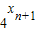 ,从而能求出数列{xn}的通项公式.
,从而能求出数列{xn}的通项公式.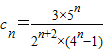 ,知
,知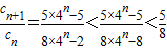 ,当n≥2时,
,当n≥2时,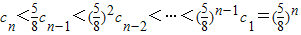 ,故T2n-1=c1+c2+…+c2n-1≤
,故T2n-1=c1+c2+…+c2n-1≤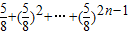 .由此能够证明
.由此能够证明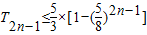 ;
; ,由
,由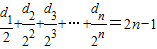 ,知
,知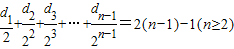 ,故
,故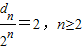 ,由此能够比较An与
,由此能够比较An与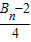 的大小.
的大小.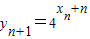 =
=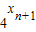 ,
,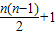 .
.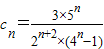 ,
,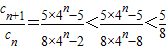 ,…(5分)
,…(5分)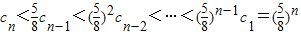 ,
,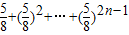 =
=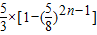 ,(当n=1时取“=”).…(8分)
,(当n=1时取“=”).…(8分)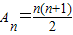 ,
,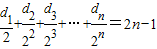 ,
,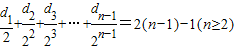 ,
,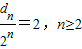 ,
,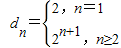 ,
,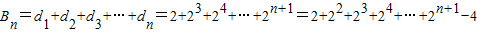
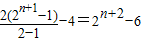 .
.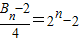 .…(10分)
.…(10分)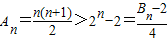 ;
;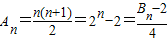
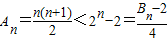
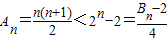
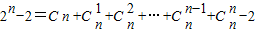 =
=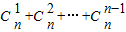
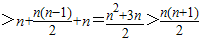 ,
, …(13分)
…(13分)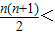 2n-2
2n-2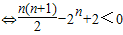
 ,
,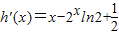 [h'(x)]'=h''(x)=1-2xln22
[h'(x)]'=h''(x)=1-2xln22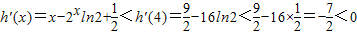
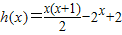 在区间[4,+∞)是减函数,
在区间[4,+∞)是减函数,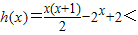
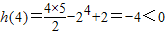
 ,即
,即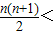 2n-2,
2n-2,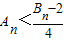 .
.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案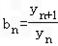 .
.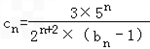 ,数列{cn}的前n项和为Tn,
,数列{cn}的前n项和为Tn, ;
;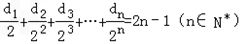 ,记数列{an}的前n项和为An,数列{dn}的前n项和为Bn,试比较An与
,记数列{an}的前n项和为An,数列{dn}的前n项和为Bn,试比较An与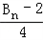 的大小.
的大小.