��������1���������P
n��������x
n��y
n-1�����Ӷ��õ�
yn+1=4xn+n=
4xn+1��x
n+1=x
n+n���ɴ����������{x
n}��ͨ�ʽ��
��2����a
n=n��
bn=4n��
cn=��֪
S1=1����
S2=1+=����
S3=1++=������n��3ʱ��
Sn=+++��+��1+
+
+
+��+
��
��
��3����n��2��k=1��2������2n-1ʱ����d
k+d
2n-k=
��[+]��
0���ɴ��ܹ��Ƶ����������n��N
*�����У�2n-1��•d
n��T
2n-1��
����⣺��1���������P
n��������x
n��y
n-1����
��
yn+1=4xn+n=
4xn+1��
��x
n+1=x
n+n��
��x
n=x
n-1+n-1
=x
n-2+��n-2��+��n-1��
=��=x
1+1+2+��+��n-1��
=
+1��
��2���ɣ�1��֪��a
n=n��
bn=4n��
��
cn=��
��
S1=1����
S2=1+=����
S3=1++=����
�൱n��3ʱ��
Sn=+++��+��1+
+
+
+��+
=1+
+
��=
+-��
��
��3����n��2��k=1��2������2n-1ʱ���У�
d
k+d
2n-k=
��[+]��
��2=
=
��
�֡�4
k+4
2n-k��2��4
n��
��4
2n-4
k-4
2n-k+1��4
2n-2��4
n+1=��4
n-1��
2��
��
dk+d2n-k����=2dn��
T2n-1����(2n-1)��2dn=��2n-1��d
n��
��������n��N
*�����У�2n-1��•d
n��T
2n-1��
���������⿼�����е�ͨ�ʽ����������������С�ıȽϣ����鲻��ʽ��֤��������ʱҪ�������⣬ע��ȼ�ת��˼��ĺ������ã�



 �ŵ������ϵ�д�
�ŵ������ϵ�д� 53������ϵ�д�
53������ϵ�д�
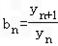 ��
��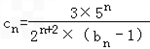 ������{cn}��ǰn���ΪTn��
������{cn}��ǰn���ΪTn�� ��
��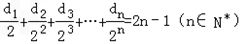 ��������{an}��ǰn���ΪAn������{dn}��ǰn���ΪBn���ԱȽ�An��
��������{an}��ǰn���ΪAn������{dn}��ǰn���ΪBn���ԱȽ�An��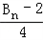 �Ĵ�С��
�Ĵ�С��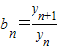 ��
��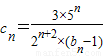 ������{cn}��ǰn���ΪTn����֤��
������{cn}��ǰn���ΪTn����֤�� ��
��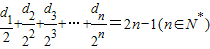 ��������{an}��ǰn���ΪAn������{dn}��ǰn���ΪBn���ԱȽ�An��
��������{an}��ǰn���ΪAn������{dn}��ǰn���ΪBn���ԱȽ�An��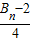 �Ĵ�С��
�Ĵ�С��