
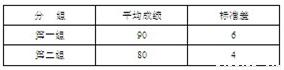
 [(x12+x22+…+xn2)-n
[(x12+x22+…+xn2)-n 2]即可求得方差,开根号求出标准差.
2]即可求得方差,开根号求出标准差.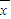 ,全班成绩的方差为s2,
,全班成绩的方差为s2, [(x12+x22++x182)-18×902]=36,
[(x12+x22++x182)-18×902]=36, [(x192+x202++x402)-22×802]=16.
[(x192+x202++x402)-22×802]=16.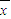 =
= (90×18+80×22)=
(90×18+80×22)=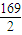 =84.5,
=84.5,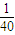 [(x12+x22++x182)+(x192+x202++x402)-40•
[(x12+x22++x182)+(x192+x202++x402)-40• 2]
2]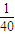 [18×(36+8100)+22×(16+6400)-40×
[18×(36+8100)+22×(16+6400)-40×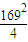 ]
]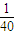 (146448+141152-10×1692)
(146448+141152-10×1692) ×1990=49.75.
×1990=49.75. ≈7.05.
≈7.05.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
统计量 组别 |
平均分 | 方差 |
| 第一组 | 80 | 16 |
| 第二组 | 90 | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 51 |
| 51 |
查看答案和解析>>
科目:高中数学 来源: 题型:
分 组 | 平均成绩 | 标准差 |
第一组 | 90 | 6 |
第二组 | 80 | 4 |
求全班的平均成绩和标准差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com