【题目】如图，四边形
是矩形，
平面，
，
为
中点.
（1）证明：平面
平面
；
（2）求异面直线
与
所成角的大小.
【答案】（1）证明见解析；（2）
【解析】
（1）由题意可证出
，利用线面垂直的定义可得PA⊥DE，再利用面面垂直的判定定理即可证出.
（2）设PA，AD的中点分别为M，N，连接MN，NC，MC，AC，从而可得
为异面直线AE与PD所成角或其补角，在
中，利用余弦定理即可求解.
（1）由题意可知AB=BE=1，
，
同理可得
，所以
所以，又因为PA⊥ABCD，所以PA⊥DE，
因为
，
所以DE⊥平面PAE，所以平面PAE⊥PDE
（2）设PA，AD的中点分别为M，N，连接MN，NC，MC，AC.
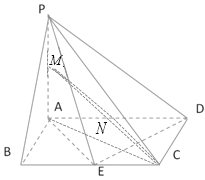
所以，NC∥AE，MN∥PD，
所以为异面直线AE与PD所成角或其补角，
由题可知
由余弦定理可得
，所以异面直线
与
所成角为
科目：高中数学 来源： 题型：
【题目】如图①，已知直角梯形ABCD中，
，
，过A作
，垂足为E.现将
沿AE折叠，使得
，如图②.
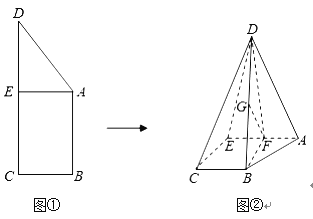
（1）求证：
；
（2）若FG分别为AE，DB的中点.
（i）求证：
平面DCE；
（ii）求证：平面
平面DBC.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】党的十八大以来，脱贫工作取得巨大成效，全国农村贫困人口大幅减少.如图的统计图反映了2012﹣2019年我国农村贫困人口和农村贫困发生率的变化情况（注：贫困发生率＝贫困人数（人）÷统计人数（人）×100%）.根据统计图提供的信息，下列推断不正确的是（ ）
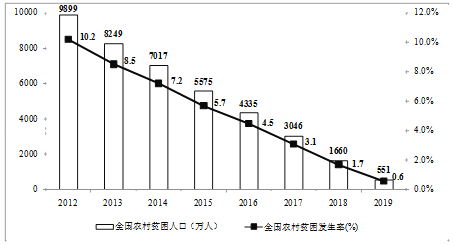
A.2012﹣2019年，全国农村贫困人口逐年递减
B.2013﹣2019年，全国农村贫困发生率较上年下降最多的是2013年
C.2012﹣2019年，全国农村贫困人口数累计减少9348万
D.2019年，全国各省份的农村贫困发生率都不可能超过0.6%
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，过动点
作直线
的垂线，垂足为
，且满足
，其中
为坐标原点，动点的轨迹为曲线
.
（Ⅰ）求曲线的方程；
（Ⅱ）过点
作与
轴不平行的直线
，交曲线于
，
两点，点
，记
，
，
分别为，
，
的斜率，求证：
为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在底面是菱形的四棱柱ABCD－A1B1C1D1中，∠ABC＝60°，AA1＝AC＝2，A1B＝A1D＝
，点E在A1D上
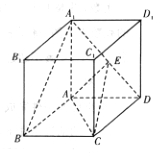
（1）求证：AA1⊥平面ABCD;
（2）当E为线段A1D的中点时，求点A1到平面EAC的距离
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】树林的边界是直线
（如图
所在的直线），一只兔子在河边喝水时发现了一只狼，兔子和狼分别位于的垂线
上的点
点和
点处，
（
为正常数），若兔子沿
方向以速度
向树林逃跑，同时狼沿线段
方向以速度
进行追击（为正常数），若狼到达
处的时间不多于兔子到达M处的时间，狼就会吃掉兔子.
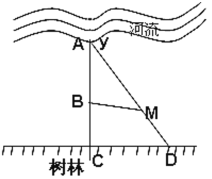
（1）求兔子的所有不幸点（即可能被狼吃掉的点）的区域面积
；
（2）若兔子要想不被狼吃掉，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的最小正周期为4
，其图象关于直线
对称，给出下面四个结论：
①函数
在区间
上先增后减；②将函数的图象向右平移
个单位后得到的图象关于原点对称；③点
是函数图象的一个对称中心；④函数在
上的最大值为1．其中正确的是( )
A. ①② B. ③④ C. ①③ D. ②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
(I)若
，判断
上的单调性；
(Ⅱ)求函数
上的最小值；
(III)当
时，是否存在正整数n，使
恒成立？若存在，求出n的最大值；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，
，过点
的直线与椭圆
交于
两点，延长
交椭圆于点
，
的周长为8.
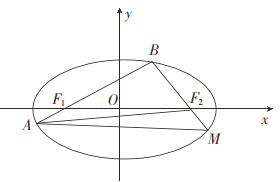
（1）求的离心率及方程；
（2）试问：是否存在定点
，使得
为定值？若存在，求
；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com