练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知双曲线x2-4y2=4,求过点A(3,-1)且被A平分的弦MN所在的直线方程.

    思路解析：设而不求，即设出A、B的坐标，联立方程组，利用韦达定理，整体消参.也可用对称性解决.

    解法一：设过A（3，-1）的直线方程为y=k(x-3)-1,

    代入双曲线方程,得x2-4［k(x-3)-1］2=4.

    整理得(4k2-1)x2-8k(3k+1)x+36k2+24k+8=0.

    若直线与双曲线交于M(x1,y1),N(x2,y2)两点，则Δ≥0,

    由韦达定理,得x1+x2=.                                                ①

    ∵A平分MN,∴=3,解得k=-,代入①验证，满足Δ≥0,

    ∴MN存在. ∴所求直线方程y=-(x-3)-1,即3x+4y-5=0.

    解法二：设M(x1,y1),N(x2,y2),则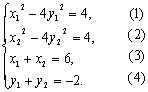

    由(1)-(2),得x12-x22=4(y12-y22),即=.

    将(3)、(4)代入上式,得kMN==-,

    故MN所在直线方程为y+1=-(x-3),

    即3x+4y-5=0,与双曲线方程x2-4y=4联立，消去y得5x2-30x+41=0.

    ∵Δ=302-820＞0,∴M、N两点存在.

    所求直线方程为3x+4y-5=0.

    解法三：设弦MN一个端点的坐标为(x,y)，则弦另一个端点的坐标为(6-x,-2-y).

    若MN存在，则M、N两点在双曲线上，

    ∴x2-4y2=4,                                                                         ①

    且(6-x)2-4(-2-y)2=4.                                                            ②

    ①-②整理,得3x+4y-5=0.

    与双曲线方程x2-4y2=4联立,消去y,得5x2-30x+41=0,

    ∵Δ=302-820＞0,∴该直线与双曲线相交于两点.

    ∴所求直线方程为3x+4y-5=0.

    误区警示

        直线与双曲线的关系中，都需要对所求直线的存在性进行验证（这一点与椭圆不同）,否则就容易出现错误.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知双曲线
    y2
    a2
    -
    x2
    b2
    =1    的一个焦点与抛物线x2=4y的焦点重合，且双曲线的实轴长是虚轴长的一半，则该双曲线的方程为（　　）
    A、5y2-
    5
    4
    x2=1
    B、
    x 2
    5
     - 
    y2
    4
    =1
    C、
    y2
    5
    -
    x2
    4
    =1
    D、5x2-
    5
    4
    y2=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线的一个焦点与抛物线x2=20y的焦点重合，且其渐近线的方程为3x±4y=0，则该双曲线的标准方程为（　　）
    A、
    x2
    9
    -
    y2
    16
    =1
    B、
    x2
    16
    -
    y2
    9
    =1
    C、
    y2
    9
    -
    x2
    16
    =1
    D、
    y2
    16
    -
    x2
    9
    =1

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省泉州市晋江市养正中学高三（上）第一次月考数学试卷（文科）（解析版） 题型：选择题

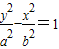    已知双曲线的一个焦点与抛物线x2=4y的焦点重合，且双曲线的实轴长是虚轴长的一半，则该双曲线的方程为（ ）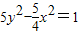
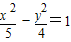
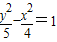
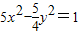
    A．
    B．
    C．
    D．

    查看答案和解析>>

    科目：高中数学 来源：2012年福建省高考数学模拟试卷1（文科）（解析版） 题型：选择题

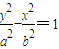    已知双曲线的一个焦点与抛物线x2=4y的焦点重合，且双曲线的实轴长是虚轴长的一半，则该双曲线的方程为（ ）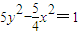
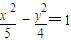
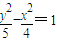
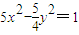
    A．
    B．
    C．
    D．

    查看答案和解析>>

    科目：高中数学 来源：2011年福建省福州三中高考数学模拟试卷（文科）（解析版） 题型：选择题

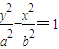    已知双曲线的一个焦点与抛物线x2=4y的焦点重合，且双曲线的实轴长是虚轴长的一半，则该双曲线的方程为（ ）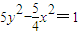
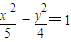
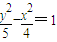
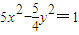
    A．
    B．
    C．
    D．

    查看答案和解析>>

    同步练习册答案