练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在平面几何中有如下性质：从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值．类比上述性质，给出立体几何中相应的性质．
    答案：略
    解析：

    解：可以从以下答案中任选一种：

    (1)从二面角的棱出发的一个半平面内任意一点到二面角的两个面的距离之比为定值．

    (2)从二面角的棱上一点出发的一条射线上任意一点到二面角的两个面的距离之比为定值．

    (3)在空间，从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值．

    (4)在空间，射线OD上任意一点P到平面AOB，BOC，COA的距离之比不变．

    (5)在空间，射线OD上任意一点P到射线OA、OB、OC的距离之比不变．

    (6)从斜足出发的一条射线上的任意一点到斜线的距离与到平面的距离之比为定值．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    6、在空间中有如下命题：
    ①互相平行的两条直线在同一平面内的射影必然是互相平行的两条直线；
    ②若平面α∥平面β，则平面α内任意一条直线m∥平面β
    ③若平面α与平面β的交线为m，平面α内一条直线n⊥直线m，则直线n⊥平面β
    ④若点P到三角形的三个顶点距离相等，则点P的该三角形所在平面的射影是该三角形的外心
    其中正确的命题个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面几何中有：Rt△ABC的直角边分别为a，b，斜边上的高为h，则
    1
    a2
    +
    1
    b2
    =
    1
    h2
    ．类比这一结论，在三棱锥P-ABC中，PA、PB、PC两两互相垂直，且PA=a，PB=b，PC=c，此三棱锥P-ABC的高为h，则结论为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

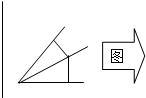    在平面几何中有如下特性：从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值．类比上述性质，请叙述在立体几何中相应地特性，并画出图形．不必证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面几何中有：Rt△ABC的直角边分别为a,b，斜边上的高为h，则.类比这一结论，在三棱锥P―ABC中，PA、PB、PC两两互相垂直，且PA=a，PB=b，PC=c，此三棱锥P―ABC的高为h，则结论为______________

    查看答案和解析>>

    同步练习册答案