数列{an}的前n项和记为Sn,a1=1,an+1=2Sn+1(n≥1).
(1)求证{an}是等比数列,并求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
解:(1)由a
n+1=2S
n+1可得a
n=2S
n-1+1(n≥2),-----(1分)
两式相减得a
n+1-a
n=2a
n,a
n+1=3a
n(n≥2).--------(3分)
又a
2=2S
1+1=3,∴a
2=3a
1.-----------(4分)
故{a
n}是首项为1,公比为3的等比数列,∴a
n=3
n-1.---(6分)
(2)设{b
n}的公差为d,
由T
3=15得b
1+b
2+b
3=15,可得b
2=5,--------(8分)
故可设b
1=5-d,b
3=5+d,
又a
1=1,a
2=3,a
3=9,
由题意可得(5-d+1)(5+d+9)=(5+3)
2,--------(10分)
解得d
1=2,d
2=-10.-----------(12分)
∵等差数列{b
n}的各项为正,∴d>0.∴d=2,-------(13分)
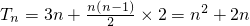
.-----------(15分)
分析:(1)利用{a
n}的通项公式,表示出第n项与第n+1项,推出二者的关系,即可判断是否是等比数列,然后求{a
n}的通项公式;
(2)设等差数列{b
n}的公差为d,各项为正,通过T
3=15,又a
1+b
1,a
2+b
2,a
3+b
3成等比数列,求出数列的公差,即可求T
n.
点评:本题是中档题,考查数列的判断,数列的定义的应用,数列的递推关系式的应用,考查学生分析问题解决问题的能力,计算能力.

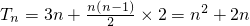 .-----------(15分)
.-----------(15分)

 阅读快车系列答案
阅读快车系列答案