
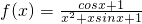 ,对于区间
,对于区间 上的任意实数x1、x2,有如下条件:
上的任意实数x1、x2,有如下条件: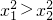 ;③|x1|>x2;④x1+x2<0;⑤x1>|x2|.
;③|x1|>x2;④x1+x2<0;⑤x1>|x2|. 上的单调性,然后利用单调性的定义验证正确的条件,列举反例判断不正确的条件即可
上的单调性,然后利用单调性的定义验证正确的条件,列举反例判断不正确的条件即可 ,
,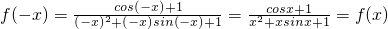
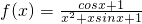 是偶函数
是偶函数 上的单调性
上的单调性
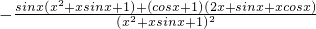
 时,sinx≥0,cosx≥0,∴f′(x)<0
时,sinx≥0,cosx≥0,∴f′(x)<0 上的单调减
上的单调减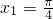 ,
,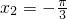 ,∴
,∴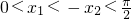 ,∴f(x1)>f(-x2),∴f(x1)>f(x2),∴①不正确;
,∴f(x1)>f(-x2),∴f(x1)>f(x2),∴①不正确;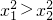 ,x1、x2∈
,x1、x2∈ ,∴
,∴ ≥|x1|>|x2|≥0,∴f(x1)<f(x2)恒成立,∴②正确;
≥|x1|>|x2|≥0,∴f(x1)<f(x2)恒成立,∴②正确; ,
,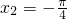 ,∴
,∴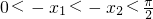 ,∴f(-x1)>f(-x2),∴f(x1)>f(x2),∴③不正确;
,∴f(-x1)>f(-x2),∴f(x1)>f(x2),∴③不正确;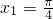 ,
,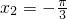 ,∴
,∴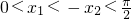 ,∴f(x1)>f(-x2),∴f(x1)>f(x2),可知④不正确
,∴f(x1)>f(-x2),∴f(x1)>f(x2),可知④不正确 上的任意实数x1、x2,即x1>x2,且x1,x2∈
上的任意实数x1、x2,即x1>x2,且x1,x2∈ ,,∴f(x1)<f(x2)恒成立,∴⑤正确;
,,∴f(x1)<f(x2)恒成立,∴⑤正确;

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源:2011年江苏省如皋市高一上学期期中考试数学 题型:填空题
下列命题正确的个数为__ ▲ ___
①若 ,则函数
,则函数 的图象不经过第三象限;
的图象不经过第三象限;
②已知函数 定义域是
定义域是 ,则
,则 的定义域是
的定义域是 ;
;
③函数 的单调减区间是
的单调减区间是
④已知集合 ,那么
,那么 ;
;
⑤已知函数 是定义在
是定义在 上的不恒为
上的不恒为 的函数,且对于任意的
的函数,且对于任意的 ,都有
,都有 ,则函数
,则函数 为奇函数.
为奇函数.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三综合检测数学理卷 题型:解答题
(本小题满分14分)
已知函数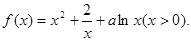
(Ⅰ)若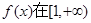 上单调递增,求a的取值范围;
上单调递增,求a的取值范围;
(Ⅱ)若定义在区间D上的函数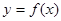 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式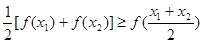 成立,则称函数
成立,则称函数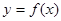 为区间D上的“凹函数”.试判断当
为区间D上的“凹函数”.试判断当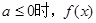 是否为“凹函数”,并对你的判断加以证明.
是否为“凹函数”,并对你的判断加以证明.
查看答案和解析>>
科目:高中数学 来源:2014届度北京市密云县高一第一学期期末数学试卷 题型:解答题
已知函数
 满足
满足 ,对于任意
,对于任意 R都有
R都有 ,且
,且  ,令
,令 .
.
(Ⅰ)求函数 的表达式;
的表达式;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)研究函数 在区间
在区间 上的零点个数.
上的零点个数.
查看答案和解析>>
科目:高中数学 来源:江西省月考题 题型:填空题
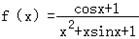 ,对于区间
,对于区间 上的任意实数x1、x2,有如下条件:
上的任意实数x1、x2,有如下条件: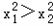 ;③|x1|>x2;④x1+x2<0;⑤x1>|x2|.
;③|x1|>x2;④x1+x2<0;⑤x1>|x2|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com