分析:解法一:(1)建立如图所示的空间直角坐标系,证明
•=0,•=0,可得BD⊥AC,BD⊥AB
1,从而可得BD⊥平面AB
1C.
(2)求出平面AB
1C
1的一个法向量,平面AB
1C的法向量,利用向量的夹角公式,可求二面角C-AB
1-C
1的余弦值;
解法二:(1)分别取AC、AB
1中点E、F,连结DE,BE,BF,DF,证明BD⊥AC,BD⊥AB
1,利用线面垂直的判定定理,即可得到结论;
(2)连结CF,证明∠DFC为二面角C-AB
1-C
1的平面角,在△DFC中,利用余弦定理可求二面角C-AB
1-C
1的余弦值.
解答: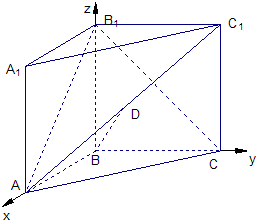
解法一:(1)建立如图所示的空间直角坐标系B-xyz,如图,
=(-1,1,1),=(-1,0,1)则B(0,0,0),A(1,0,0),C(0,1,0),B
1(0,0,1),C
1(0,1,1),D(
,,).
则
=(,,),
=(-1,1,0),=(-1,0,1).
∴
•=0,•=0.
∴BD⊥AC,BD⊥AB
1,且AC∩AB
1=A.
∴BD⊥平面AB
1C.
(2)设平面AB
1C
1的一个法向量为
=(x,y,z)∴
⊥,⊥∴
•=0,•=0即有
令x=1,得
=(1,0,1)由(1)可知
=(,,)是平面AB
1C的法向量
cos<,>===.
即二面角C-AB
1-C
1的余弦值为
.
解法二:
(1)分别取AC、AB
1中点E、F,连结DE,BE,BF,DF,
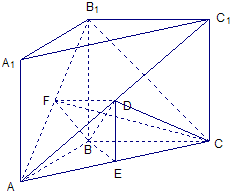
∵D、F是AC
1、AB
1的中点,则DE∥CC
1,DF∥B
1C
1∵CC
1⊥平面ABC,∴DE⊥平面ABC.
则BE是BD在平面ABC内的射影.
∵AB=BC,∴BE⊥AC.
∴BD⊥AC
∵B
1C
1⊥BB
1,B
1C
1⊥A
1B
1,BB
1∩A
1B
1=B
1∴B
1C
1⊥平面ABB
1∴DF⊥平面ABB
1则BF是BD在平面ABB
1内的射影.
∵AB=BB
1,∴BF⊥AB
1.
∴BD⊥AB
1.
又AC∩AB
1=A,
∴BD⊥平面AB
1C.
(2)连结CF.
由(1)知,DF⊥平面ABB
1,∴DF⊥AB
1∵
AC=B1C=,∴CF⊥AB
1.
则∠DFC为二面角C-AB
1-C
1的平面角.
在△DFC中,
CF=×=,DF=B1C1=,CD=AC1=,
则
cos∠DFC==.
即二面角C-AB
1-C
1的余弦值为
.
点评:本题考查线面垂直,考查面面角,考查学生分析解决问题的能力,考查向量知识的运用,属于中档题.

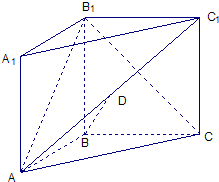 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1=1,点D是AC1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1=1,点D是AC1的中点. 解法一:(1)建立如图所示的空间直角坐标系B-xyz,如图,
解法一:(1)建立如图所示的空间直角坐标系B-xyz,如图,






