[题目]齐王与田忌赛马.每场比赛三匹马各出场一次.共赛三次.以胜的次数多者为赢．田忌的上马优于齐王的中马.劣于齐王的上马.田忌的中马优于齐王的下马.劣于齐王的中马.田忌的下马劣于齐王的下马．现各出上.中.下三匹马分组进行比赛.如双方均不知对方马的出场顺序.则田忌获胜的概率是( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】齐王与田忌赛马，每场比赛三匹马各出场一次，共赛三次，以胜的次数多者为赢．田忌的上马优于齐王的中马，劣于齐王的上马，田忌的中马优于齐王的下马，劣于齐王的中马，田忌的下马劣于齐王的下马．现各出上、中、下三匹马分组进行比赛，如双方均不知对方马的出场顺序，则田忌获胜的概率是（）
A.
B.
C.
D.

【答案】B
【解析】解：记齐王的三匹马分别为A、B、C，记田忌的三匹马分别为a、b、c．

若A与a比赛，记为Aa，齐王与田忌赛马，有如下六种情况：

Aa，Bb，Cc；Aa，Bc，Cb；Ab，Bc，Ca；Ab，Ba，Cc；Ac，Ba，Cb；Ac，Bb，Ca．

其中田忌获胜的只有一种：Ac，Ba，Cb．

∴田忌获胜的概率为．

故选：B．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知向量 =（cosωx﹣sinωx，sinωx）， =（﹣cosωx﹣sinωx，2 cosωx），设函数f（x）= +λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（，1）
（1）求函数f（x）的最小正周期；
（2）若y=f（x）的图象经过点（，0）求函数f（x）在区间[0， ]上的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若函数f（x）满足对于任意实数a，b，c，都有f（a），f（b），f（c）为某三角形的三边长，则成f（x）为“可构造三角形函数”，已知f（x）= 是“可构造三角形函数”，则实数t的取值范围是（）
A.[﹣1，0]
B.（﹣∞，0]
C.[﹣2，﹣1]
D.[﹣2，﹣ ]

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知A为椭圆 =1（a＞b＞0）上的一个动点，弦AB，AC分别过左右焦点F1 ， F2 ，且当线段AF1的中点在y轴上时，cos∠F1AF2= ．（Ⅰ）求该椭圆的离心率；
（Ⅱ）设，试判断λ1+λ2是否为定值？若是定值，求出该定值，并给出证明；若不是定值，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，点A，B是单位圆O上的两点，A，B点分别在第一，而象限，点C是圆O与x轴正半轴的交点，若∠COA=60°，∠AOB=α，点B的坐标为（﹣ ，）．
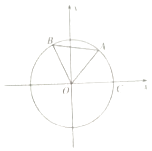
（1）求sinα的值；
（2）已知动点P沿圆弧从C点到A点匀速运动需要2秒钟，求动点P从A点开始逆时针方向作圆周运动时，点P的纵坐标y关于时间t（秒）的函数关系式．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某研究机构对中学生记忆能力x和识图能力y进行统计分析，得到如下数据：

记忆能力x	4	6	8	10
识图能力y	3	﹡﹡﹡	6	8

由于某些原因，识图能力的一个数据丢失，但已知识图能力样本平均值是5.5．
（Ⅰ）求丢失的数据；
（Ⅱ）经过分析，知道记忆能力x和识图能力y之间具有线性相关关系，请用最小二乘法求出y关于x的线性回归方程；
（III）若某一学生记忆能力值为12，请你预测他的识图能力值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知抛物线y2=2px（p＞0），F为其焦点，l为其准线，过F作一条直线交抛物线于A，B两点，A′，B′分别为A，B在l上的射线，M为A′B′的中点，给出下列命题： ①A′F⊥B′F；
②AM⊥BM；
③A′F∥BM；
④A′F与AM的交点在y轴上；
⑤AB′与A′B交于原点．
其中真命题的是．（写出所有真命题的序号）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】过点（1，2）总可以作两条直线与圆 x2+y2+kx+2y+k2﹣15=0 相切，则实数k的取值范围是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若椭圆与双曲线有相同的焦点F1、F2 ， P是两曲线的一个交点，则△F1PF2的面积是（）
A.4
B.2
C.1
D.

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学