
| A. | $\frac{15}{2}$ | B. | $\frac{13}{2}$ | C. | $\frac{31}{2}$ | D. | $\frac{51}{2}$ |
分析 根据c>0,b2=ac,判断,a,b,c成等比数列,利用等比数列的性质,转化为以公比q为变量的函数,利用基本不等式的性质进行求解即可.
解答 解:∵c>0,b2=ac,
∴a>0,
∵3b≥2a+c,
∴b>0,
则a,b,c成等比数列,设公比为q,(q>0),
则c=aq2,b=aq,
由3b≥2a+c得3aq≥2a+aq2,
即q2-3q+2≤0,
即1≤q≤2,
则$\frac{4a+2b+c}{a+b}$=$\frac{4a+2aq+a{q}^{2}}{a+aq}$=$\frac{{q}^{2}+2q+4}{1+q}$=$\frac{(q+1)^{2}+3}{q+1}$=(q+1)+$\frac{3}{q+1}$
设t=q+1,则2≤t≤3,
则y=t+$\frac{3}{t}$则2≤t≤3为增函数,
∴当t=2时,取得最小值y=2+$\frac{3}{2}$=$\frac{7}{2}$,当t=3时,取得最大值y=3+1=4,
则$\frac{4a+2b+c}{a+b}$的最大值与最小值之和为4+$\frac{7}{2}$=$\frac{15}{2}$,
故选:A
点评 本题主要考查函数最值的求解,根据不等式的关系,转化为等比数列,结合基本不等式的性质是解决本题的关键.综合性较强,难度较大.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
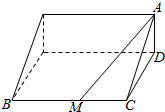 如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.
如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
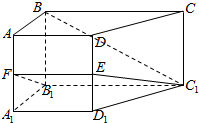 如图所示,在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=$\sqrt{2}$,AD=2,BC=4,AA1=2,E、F分别是DD1,AA1的中点.
如图所示,在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=$\sqrt{2}$,AD=2,BC=4,AA1=2,E、F分别是DD1,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com