Question

已知f（x）=|x²-4x-5|
（1）求函数f（x）的零点；
（2）讨论方程|x²-4x-5|=K（K∈R）的解的情况．

Answer 1

解：（1）令f（x）=|x²-4x-5|=0
即x²-4x-5=0
解得x=-1，或x=5，
即函数f（x）的零点为-1和5．
（2）函数f（x）的图象如图所示：

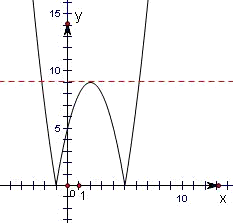
由图得：
当k＜0时，f（x）=|x²-4x-5|的图象与y=k无交点，则方程|x²-4x-5|=k无解；
当k=0，或k＞9时，f（x）=|x²-4x-5|的图象与y=k有两个交点，则方程|x²-4x-5|=k有两解；
当0＜k＜9时，f（x）=|x²-4x-5|的图象与y=k有四个交点，则方程|x²-4x-5|=k有四解；
当k=9时，f（x）=|x²-4x-5|的图象与y=k有三个交点，则方程|x²-4x-5|=k有三解．
分析：（1）根据函数零点与方程根之间的关系，解方程|x²-4x-5|=0，即可求出函数f（x）的零点；
（2）根据二次函数的图象和性质及对折变换法则，我们易画出函数f（x）的图象，根据图象，分别讨论f（x）=|x²-4x-5|的图象与y=k交点的个数，即可得到方程|x²-4x-5|=k的解的情况．
点评：本题考查的知识点是函数图象的作法，函数的零点，根的存在性及根的个数的判断，其中（2）中的数形结合是高中的第一大数学思想，要引起大家的重视．