
在直角坐标系 中,动点
中,动点 与定点
与定点 的距离和它到定直线
的距离和它到定直线 的距离之比是
的距离之比是 ,设动点
,设动点 的轨迹为
的轨迹为 ,
, 是动圆
是动圆
 上一点.
上一点.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设曲线 上的三点
上的三点 与点
与点 的距离成等差数列,若线段
的距离成等差数列,若线段 的垂直平分线与
的垂直平分线与 轴的交点为
轴的交点为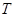 ,求直线
,求直线 的斜率
的斜率 ;
;
(3)若直线 与
与 和动圆
和动圆 均只有一个公共点,求
均只有一个公共点,求 、
、 两点的距离
两点的距离 的最大值.
的最大值.
(1)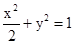 ;(2)
;(2)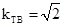 ;(3)
;(3)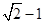 .
.
【解析】本试题主要考查了轨迹方程的求解和椭圆的定义,以及直线与椭圆的位置关系的综合运用。
解:(1)由已知,得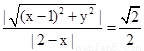 ,…………………………1分.
,…………………………1分.
将两边平方,并化简得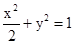 , …………………………3分.
, …………………………3分.
故轨迹C1的方程是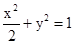 。
………………4分.
。
………………4分.
(2)由已知可得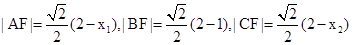 ,,,
,,,
因为2|BF|=|AF|=|CF|,所以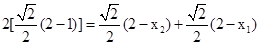
即得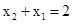 , ①
…………………………5分.
, ①
…………………………5分.
故线段AC的中点为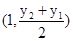 ,其垂直平分线方程为
,其垂直平分线方程为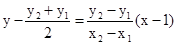 , ②
, ②
…………………………6分.
因为A,C在椭圆上,故有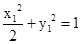 ,
,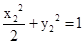 ,两式相减,
,两式相减,
得: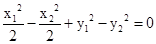 ③
③
将①代入③,化简得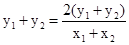 , ④ ………………………7分.
, ④ ………………………7分.
将④代入②,并令y=0得,x=1/2,即T的坐标为(1/2,0)。………………………8分.
所以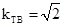 .
………………………9分.
.
………………………9分.
设 、
、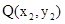 ,直线
,直线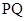 的方程为
的方程为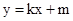
因为P既在椭圆C1上又在直线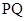 上,从而有
上,从而有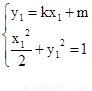
将(1)代入(2)得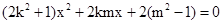 ………10分.
………10分.
由于直线PQ与椭圆C1相切,故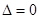
从而可得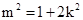 ,
,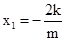 (3)
(3)
同理,由Q既在圆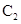 上又在直线
上又在直线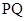 上,可得
上,可得
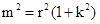 ,
,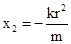 (4)……………………12分
(4)……………………12分
由(3)、(4)得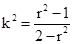 ,
,
所以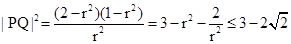 ……………………13分.
……………………13分.
即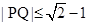 ,当且仅当
,当且仅当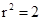 时取等号,
时取等号,
故P,Q、两点的距离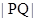 的最大值
的最大值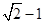 . …………………………14分.
. …………………………14分.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共12分)
在直角坐标系![]() 中,动点P到两定点
中,动点P到两定点![]() ,
,![]() 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为![]() ,过点
,过点![]() 的直线与
的直线与![]() 交于A,B两点.
交于A,B两点.
(1)写出![]() 的方程;
的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值;若存在, 求出d的最大值、最小值.
查看答案和解析>>
科目:高中数学 来源:长葛市第三实验高中2010年高考模拟试卷(1) 题型:解答题
(本小题共12分)
在直角坐标系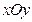 中,动点P到两定点
中,动点P到两定点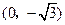 ,
,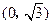 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为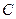 ,过点
,过点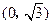 的直线与
的直线与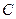 交于A,B两点.
交于A,B两点.
(1)写出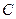 的方程;
的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值;若存在,求出d的最大值、最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市西城区高三4月第一次模拟考试理科数学(解析版) 题型:填空题
在直角坐标系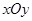 中,动点
中,动点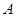 ,
,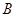 分别在射线
分别在射线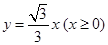 和
和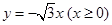 上运动,且△
上运动,且△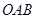 的面积为
的面积为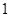 .则点
.则点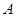 ,
,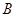 的横坐标之积为_____;△
的横坐标之积为_____;△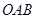 周长的最小值是_____.
周长的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com