练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，D、E在线段BC上，且BD=EC，

    求证：

     

    【答案】

    可先证

    【解析】试题分析：，∵,

    又∵BD=EC∴

    ∴

    ∴

    考点：平面向量的加减运算法则

    点评：解决本题的关键是把转化为来证。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB．
    （Ⅰ）求证：CE⊥平面PAD；
    （Ⅱ）若PA=AB=1，AD=3，CD=
    		2
    ，∠CDA=45°，求四棱锥P-ABCD的体积．
    （Ⅲ）在满足（Ⅱ）的条件下求二面角B-PC-D的余弦值的绝对值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

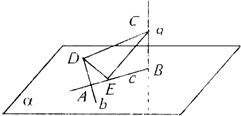    （2007•青岛一模）如图所示，b、c在平面α内，a∩c=B，b∩c=A，且a⊥b，a⊥c，b⊥c，若C∈a，D∈b，E在线段AB上（C，D，E均异于A，B），则△CDE是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

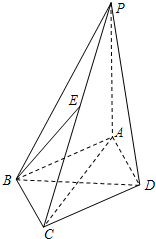    （2012•台州一模）如图，在底面为菱形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=4
    		3
    ，BD=2，AC=4，点E在线段PC上．
    （Ⅰ）当点E为线段PC的中点时，求证：BE⊥AC；
    （Ⅱ）若二面角B-EA-D为直二面角，求直线BE与平面ABCD所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

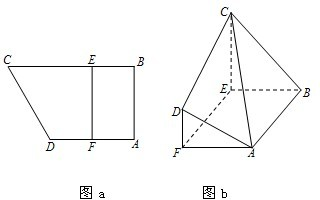    如图a所示，在直角梯形ABCD中，AB⊥AD，AD∥BC，F为AD的中点，E在BC上，且EF∥AB．已知AB=AD=CE=2，沿线段EF把四边形CDEF折起如图b所示，使平面CDEF⊥平面ABEF．
    （1）求证：AF⊥平面CDEF；
    （2）求三棱锥C-ADE的体积；
    （3）求二面角B-AC-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在图1至图3中，点B是线段AC的中点，点D是线段CE的中点。四边形BCGF和CDHN都是正方形，AE的中点是M。

    （1）如图1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，求证：FM = MH，FM⊥MH；

    （2）将图1中的CE绕点C顺时针旋转一个锐角，得到图2，求证：△FMH是等腰直角三角形；

    （3）将图2中的CE缩短到图3的情况，△FMH还是等腰直角三角形吗？（直接写出结论，不必证明）。

    查看答案和解析>>

    同步练习册答案