
一个口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试用概率说明理由.
(1)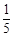 (2)这种游戏规则不公平
(2)这种游戏规则不公平
解析试题分析:解:(I)设“甲胜且两数字之和为6”为事件A,事件A包含的基本事件为(1,5),(2,4),(3,3),(4,2),(5,1),共5个.又甲、乙二人取出的数字共有5×5=25(个)等可能的结果,所以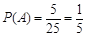 . 答:编号的和为6的概率为
. 答:编号的和为6的概率为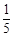 。(6分)
。(6分)
(Ⅱ)这种游戏规则不公平.(7分)
设“甲胜”为事件B,“乙胜”为事件C,则甲胜即两数字之和为偶数所包含的基本事件数为13个:(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5)(4,2) ,(4,4),(5,1) ,(5,3),(5,5).
所以甲胜的概率P(B)=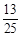 ,从而乙胜的概率P(C)=1-
,从而乙胜的概率P(C)=1-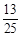 =
=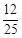 .
.
由于P(B)≠P(C),所以这种游戏规则不公平.(12分)
考点:古典概型
点评:主要是考查了随机事件的 概率的求解运用,属于基础题。


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
某市直小学为了加强管理,对全校教职工实行新的临时事假制度:“每位教职工每月在正常的工作时间,临时有事,可请假至多三次,每次至多一小时”.现对该制度实施以来50名教职工请假的次数进行调查统计,结果如下表所示:
| 请假次数 |  | 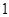 | 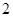 | 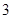 |
| 人数 | 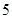 | 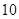 | 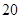 | 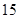 |
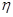 表示这两人请假次数之和,记“函数
表示这两人请假次数之和,记“函数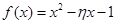 在区间
在区间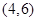 上有且只有一个零点”为事件
上有且只有一个零点”为事件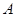 ,求事件
,求事件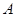 发生的概率
发生的概率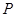 ;
;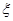 表示这两人请假次数之差的绝对值,求随机变量
表示这两人请假次数之差的绝对值,求随机变量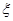 的分布列及数学期望
的分布列及数学期望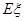 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在人寿保险业中,要重视某一年龄的投保人的死亡率,经过随机抽样统计,得到某市一个投保人能活到75岁的概率为0.60,试问:
(1)若有3个投保人, 求能活到75岁的投保人数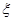 的分布列;
的分布列;
(2)3个投保人中至少有1人能活到75岁的概率.(结果精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校有甲、乙、丙三名学生报名参加2012年高校自主招生考试,三位同学通过自主招生考试考上大学的概率分别是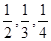 ,且每位同学能否通过考试时相互独立的。
,且每位同学能否通过考试时相互独立的。
(Ⅰ)求恰有一位同学通过高校自主招生考试的概率;
(Ⅱ)若没有通过自主招生考试,还可以参加2012年6月的全国统一考试,且每位同学通过考试的概率均为 ,求这三位同学中恰好有一位同学考上大学的概率。
,求这三位同学中恰好有一位同学考上大学的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知男人中有5%患色盲,女人中有0.25%患色盲,从100个男人和100个女人中任选一人.
(1)求此人患色盲的概率;
(2)如果此人是色盲,求此人是男人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于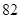 为正品,小于
为正品,小于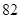 为次品.现随机抽取这两种元件各
为次品.现随机抽取这两种元件各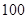 件进行检测,检测结果统计如下:
件进行检测,检测结果统计如下:
| 测试指标 | 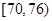 | 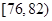 | 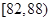 | 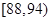 | 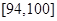 |
| 元件A | 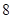 | 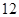 | 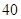 | 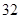 | 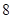 |
| 元件B | 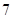 | 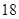 | 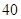 | 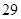 | 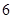 |
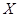 为生产1件元件A和1件元件B所得的总利润,求随机变量
为生产1件元件A和1件元件B所得的总利润,求随机变量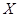 的分布列和数学期望;
的分布列和数学期望;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设有关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2) 若 是从区间[0,3] 任 取 的一个数,
是从区间[0,3] 任 取 的一个数,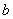 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我区高三期末统一测试中某校的数学成绩分组统计如下表:
| 分组 | 频数 | 频率 |
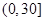 | 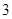 | 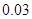 |
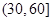 | 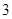 | 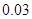 |
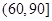 | 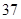 | 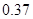 |
 | 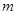 | 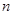 |
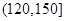 | 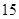 | 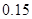 |
| 合计 | 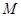 | 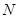 |
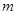 、
、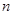 、
、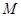 、
、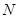 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;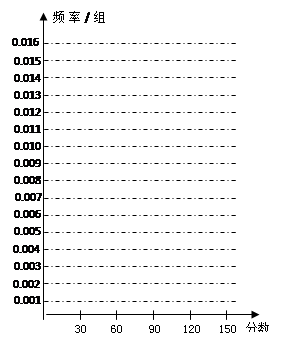
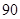 分以上的人数;
分以上的人数;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数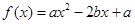 (
(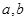
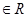 )
)
(1)若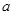 从集合
从集合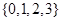 中任取一个元素,
中任取一个元素,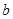 从集合
从集合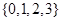 中任取一个元素,
中任取一个元素,
求方程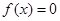 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若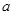 从区间
从区间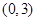 中任取一个数,
中任取一个数,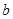 从区间
从区间 中任取一个数
中任取一个数
求方程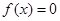 没有实根的概率.
没有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com