
 的左、右焦点,P为椭圆C上任意一点,且
的左、右焦点,P为椭圆C上任意一点,且 最小值为0.
最小值为0.
 坐标关于x、y的形式,从而得到
坐标关于x、y的形式,从而得到 ,结合点P为椭圆C上的点,化简得
,结合点P为椭圆C上的点,化简得 ,说明
,说明 最小值为1-c2=0,从而解出a2=2且b2=1,得到椭圆C的方程.
最小值为1-c2=0,从而解出a2=2且b2=1,得到椭圆C的方程. ,
, -------------(1分)
-------------(1分)
 ,可得y2=
,可得y2= x2,
x2, -------------(2分)
-------------(2分) 最小值为1-c2=0,解之得c=1,可得a2=2,-------------------(3分)
最小值为1-c2=0,解之得c=1,可得a2=2,-------------------(3分) .---------------------------------------------(4分)
.---------------------------------------------(4分) ,即|k2t2-m2|=k2+1,---------------------------------(10分)
,即|k2t2-m2|=k2+1,---------------------------------(10分) 和
和 ,---------------------------(13分)
,---------------------------(13分) ;定点(1,0)到直线l1,l2的距离之积为
;定点(1,0)到直线l1,l2的距离之积为 ,也符合题意.
,也符合题意. 最小值为0的情况下求椭圆的方程,并讨论x轴上存在定点B到l1,l2的距离之积恒为1的问题,着重考查了椭圆的标准方程与简单几何性质、点到直线的距离公式、向量数量积运算和直线与圆锥曲线的位置关系等知识点,属于中档题.
最小值为0的情况下求椭圆的方程,并讨论x轴上存在定点B到l1,l2的距离之积恒为1的问题,着重考查了椭圆的标准方程与简单几何性质、点到直线的距离公式、向量数量积运算和直线与圆锥曲线的位置关系等知识点,属于中档题. 

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
 (2013•揭阳一模)如图,设点F1(-c,0)、F2(c,0)分别是椭圆C:
(2013•揭阳一模)如图,设点F1(-c,0)、F2(c,0)分别是椭圆C:| x2 |
| a2 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•揭阳一模)如图,设点F1(-c,0)、F2(c,0)分别是椭圆C:
(2013•揭阳一模)如图,设点F1(-c,0)、F2(c,0)分别是椭圆C:| x2 |
| a2 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
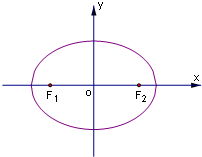 如图,设点F1(-c,0)、F2(c,0)分别是椭圆
如图,设点F1(-c,0)、F2(c,0)分别是椭圆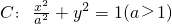 的左、右焦点,P为椭圆C上任意一点,且
的左、右焦点,P为椭圆C上任意一点,且 最小值为0.
最小值为0.查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省汕头市金山中学高三(上)开学摸底数学试卷(文科)(解析版) 题型:解答题
 的左、右焦点,P为椭圆C上任意一点,且
的左、右焦点,P为椭圆C上任意一点,且 最小值为0.
最小值为0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com