
�ĸ↑���������ҹ��ߵȽ�����ҵ����Ѹ�ٷ�չ���������ǵõ���ijʡ��
1990��2000��18��24���������ÿ�꿼���ѧ�İٷֱȣ����ǰ�ũ�塢����ͳ��зֿ�ͳ�ƣ�Ϊ�˱��ڼ��㣬��1990����Ϊ0��1991����Ϊ1����2000����Ϊ10�������ÿ�꿼���ѧ�İٷֱ���Ϊ�����������ݴ�0��10��Ϊ�Ա������лع�������ɵõ����������ع�ֱ�ߣ�����
����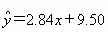 ��
��
����
����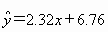 ��
��
����
ũ��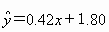 ��
��
(1)
��ͬһ������ϵ�����������ع�ֱ�ߣ�(2)
����ũ������������ϵ������0.42��ζ��ʲô?(3)
����һ�Σ���������һ���Ĵ�ѧ��ѧ�����������?(4)
������ҹ��˿ڷֲ����й����ϣ�ѡ��һ���ڸߵȽ�����չ���д����Ե�ʡ�������ʡ�Ĵ�ѧ��ѧ����Ϊ������˵���ҹ���1991��2000��10����ѧ��ѧ�ʵ����巢չ����� ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
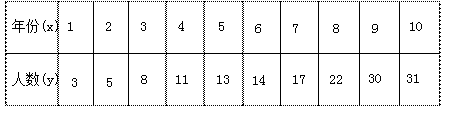
| ��ݣ�x�� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ������y�� | 3 | 5 | 8 | 11 | 13 | 14 | 17 | 22 | 30 | 31 |
 |
| b |
 |
| a |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ���x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ����y | 3 | 5 | 8 | 11 | 13 | 14 | 17 | 22 | 30 | 31 |
| ? |
| b |
| ? |
| a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ��ݣ�x�� | 1 | 2 | 3 | 4 | 5 |
| ������y�� | 3 | 5 | 8 | 11 | 13 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
. |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�������ʡ�����е���У������һ��ģ�⿼����ѧ���� ���ͣ������
����С������12�֣�
�ĸ↑���������ҹ��ߵȽ�����ҵ����ͻ���ͽ��ķ�չ�����˼�¼��ij�� ��
�� ��ʮ���ÿ�꿼���ѧ������.
��ʮ���ÿ�꿼���ѧ������. Ϊ������㣬
Ϊ������㣬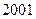 ����Ϊ
����Ϊ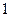 ��
��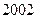 ����Ϊ
����Ϊ ������
������ ����Ϊ
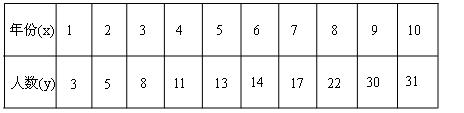
����Ϊ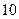 .��������:
.��������: 
������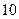 ���������ȡ���꣬�����ѧ����������
���������ȡ���꣬�����ѧ����������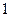 �����
�����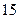 �˵ĸ��ʣ�
�˵ĸ��ʣ�
������ǰ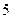 ������ݣ�������С���˷����
������ݣ�������С���˷����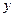 ����
����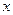 �Ļع鷽��
�Ļع鷽��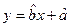 ���������
���������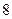 ��Ĺ���ֵ��ʵ��ֵ֮��IJ�ľ���ֵ��
��Ĺ���ֵ��ʵ��ֵ֮��IJ�ľ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�������ʡ�����и�����һ��ģ�⿼����ѧ���� ���ͣ������
������С������12�֣�
�ĸ↑���������ҹ��ߵȽ�����ҵ����ͻ���ͽ��ķ�չ�����˼�¼��ij��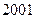 ��
��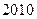 ��ʮ���ÿ�꿼���ѧ������.Ϊ������㣬
��ʮ���ÿ�꿼���ѧ������.Ϊ������㣬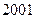 ����Ϊ
����Ϊ ��
��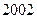 ����Ϊ
����Ϊ ������
������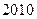 ����Ϊ
����Ϊ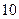 .��������:
.��������: 
������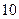 ���������ȡ���꣬�����ѧ����������
���������ȡ���꣬�����ѧ���������� �����
�����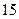 �˵ĸ��ʣ�
�˵ĸ��ʣ�
������ǰ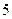 ������ݣ�������С���˷����
������ݣ�������С���˷����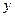 ����
���� �Ļع鷽��
�Ļع鷽��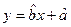 ���������
���������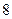 ��Ĺ���ֵ��ʵ��ֵ֮��IJ�ľ���ֵ��
��Ĺ���ֵ��ʵ��ֵ֮��IJ�ľ���ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com