
【题目】如图,在五面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() 为等边三角形,且平面
为等边三角形,且平面![]() 平面
平面![]() ,
, ![]() .
.
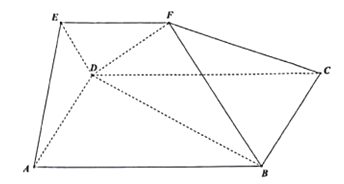
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)取DE中点G,于是AG⊥DE,由面面垂直的性质定理可得AG⊥面CDEF,则AG⊥DC,又CD⊥AD,由线面垂直的判断定理可得CD⊥面ADE,即面ADE⊥面ABCD.
(2)取AD中点O,以O为坐标原点,OA、OE为x、z轴建系.由题意可得:平面FBC的法向量为![]() ,平面BCD的法向量为
,平面BCD的法向量为![]() ,则二面角F-BC-D的余弦值为
,则二面角F-BC-D的余弦值为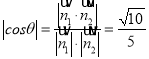 .
.
试题解析:
(1)证明:取DE中点G,于是AG⊥DE,
又面ADE⊥面CDEF,且面ADE∩面CDEF=DE,所以AG⊥面CDEF,
则AG⊥DC,又CD⊥AD,所以CD⊥面ADE,
即面ADE⊥面ABCD.
(2)解:取AD中点O,于是EO⊥面ABCD,所以,如图:
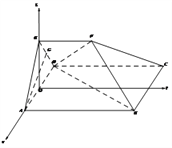
以O为坐标原点,OA、OE为x、z轴建系.设OA长度为1,
于是点坐标为: ![]() ,
,
因为CD∥AB,所以AB∥平面CDEF,又平面ABEF∩平面CDEF=EF,则EF∥AB;
所以设![]() ,所以点
,所以点![]() .
.
那么![]() ,由于BF⊥DF,
,由于BF⊥DF,
所以![]() ,解得
,解得![]() .于是
.于是![]() ,
,
进而面FBC的法向量为![]() ,
,
又面BCD的法向量为![]() ,记二面角F-BC-D为
,记二面角F-BC-D为![]() ,所以
,所以
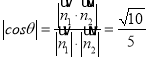 ,又因为是锐角,所以二面角F-BC-D的余弦值为
,又因为是锐角,所以二面角F-BC-D的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:
点,则翻折后的几何体中有如下描述:
①![]() 与
与![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ;
;
③![]() 是
是![]() ;
;
④平面![]() 平面
平面![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角为30°.
所成角为30°.
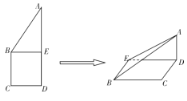
其中正确的有________.(填写你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线的图象关于![]() 轴对称,顶点在坐标原点,点
轴对称,顶点在坐标原点,点![]() 在抛物线上.
在抛物线上.
(1)求抛物线的标准方程;
(2)设直线![]() 的方程为
的方程为![]() ,若直线
,若直线![]() 与抛物线交于
与抛物线交于![]() 两点,且以
两点,且以![]() 为直径的圆过点
为直径的圆过点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,底面ABC为正三角形,
中,底面ABC为正三角形,![]() 底面ABC,
底面ABC,![]() ,点
,点![]() 在线段
在线段![]() 上,平面
上,平面![]() 平面
平面![]() .
.

(1)请指出点![]() 的位置,并给出证明;
的位置,并给出证明;
(2)若![]() ,求
,求![]() 与平面ABE夹角的正弦值.
与平面ABE夹角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com