
【题目】已知![]() 为正整数,数列
为正整数,数列![]() 满足
满足![]() ,
,![]() ,设数列
,设数列![]() 满足
满足![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)若数列![]() 是等差数列,前
是等差数列,前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;
;
(3)当![]() N*,对任意的
N*,对任意的![]() N*,均存在
N*,均存在![]() N*,使
N*,使![]() .
.
【解析】试题分析:(1)将![]() 经过移项、两边同时除以
经过移项、两边同时除以![]() 可得
可得![]() ,故可得结论
,故可得结论![]() 为等比数列;(2)由(1)得
为等比数列;(2)由(1)得![]() ,代入得
,代入得![]() ,由数列
,由数列![]() 是等差数列易知
是等差数列易知![]() ,代入可解得
,代入可解得![]() ,
,![]() ,将其进行检验得结果;
,将其进行检验得结果;
(3)由(2)得![]() ,利用等差数列前
,利用等差数列前![]() 项和公式代入
项和公式代入![]() ,解出
,解出![]() ,经讨论当
,经讨论当![]() 时符合题意,当
时符合题意,当![]() 时不符合题意.
时不符合题意.
试题解析:(1)由题意得![]() ,因为数列
,因为数列![]() 各项均正,
各项均正,
得![]() ,所以
,所以![]() ,
,
因此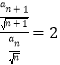 ,以
,以![]() 是以
是以![]() 为首项公比为2的等比数列.
为首项公比为2的等比数列.
(2)由(1)得![]() ,
,![]() ,
,![]() ,
,
如果数列![]() 是等差数列,则
是等差数列,则![]() ,
,
得:![]() ,即
,即![]() ,则
,则![]() ,
,
解得 ![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,
![]() ,数列
,数列![]() 是等差数列,符合题意;
是等差数列,符合题意;
当![]() =12时,
=12时,![]() ,
,
![]() ,
,![]() ,
,
![]() ,数列
,数列![]() 不是等差数列,
不是等差数列,![]() =12不符合题意;
=12不符合题意;
综上,如果数列![]() 是等差数列,
是等差数列,![]() .
.
(3)由(2)得![]() ,对任意的
,对任意的![]() N*,均存在
N*,均存在![]() N*,使
N*,使![]() ,
,
则![]() ,所以
,所以![]() .
.
当![]() ,
,![]() N*,此时
N*,此时![]() ,对任意的
,对任意的![]() N*,符合题意;
N*,符合题意;
当![]() ,
,![]() N*,当
N*,当![]() 时,
时,![]() . 不合题意.
. 不合题意.
综上,当![]() N*,对任意的
N*,对任意的![]() N*,均存在
N*,均存在![]() N*,使
N*,使![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】社会调查人员希望从对人群的随机抽样调查中得到对他们所提问题诚实的回答,但是被采访者常常不愿意如实做出应答.
1965年Stanley·L.Warner发明了一种应用概率知识来消除这种不愿意情绪的方法.Warner的随机化应答方法要求人们随机地回答所提问题中的一个,而不必告诉采访者回答的是哪个问题,两个问题中有一个是敏感的或者是令人为难的,另一个是无关紧要的,这样应答者将乐意如实地回答问题,因为只有他知道自己回答的是哪个问题.
假如在调查运动员服用兴奋剂情况的时候,无关紧要的问题是:你的身份证号码的尾数是奇数吗;敏感的问题是:你服用过兴奋剂吗.然后要求被调查的运动员掷一枚硬币,如果出现正面,就回答第一个问题,否则回答第二个问题.
例如我们把这个方法用于200个被调查的运动员,得到56个“是”的回答,请你估计这群运动员中大约有百分之几的人服用过兴奋剂.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图像与函数h(x)=![]() 的图像关于点A(0,1)对称。
的图像关于点A(0,1)对称。
(1)求函数f(x)的解析式;
(2)若g(x)=xf(x)+ax,且g(x)在区间(0,4]上为减函数,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
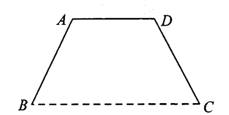
【题目】某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门![]() (如图).设计要求彩门的面积为
(如图).设计要求彩门的面积为![]() (单位:
(单位:![]() ),高为
),高为![]() (单位:
(单位:![]() )(
)(![]() 为常数).彩门的下底
为常数).彩门的下底![]() 固定在广场底面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为
固定在广场底面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为![]() ,不锈钢支架的长度和记为
,不锈钢支架的长度和记为![]() .
.
(1)请将![]() 表示成关于
表示成关于![]() 的函数
的函数![]() ;
;
(2)问当![]() 为何值
为何值![]() 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,P在对角线BD1上,且BP=![]() BD1,给出下面四个命题:
BD1,给出下面四个命题:
(1)MN∥平面APC;(2)C1Q∥平面APC;(3)A,P,M三点共线;(4)平面MNQ∥平面APC.正确的序号为 ( )
A. (1)(2) B. (1)(4) C. (2)(3) D. (3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 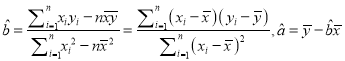 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有 ![]() 名男生,
名男生, ![]() 名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数
名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数
字)
(1)排成前后两排,前排 ![]() 人,后排
人,后排 ![]() 人;
人;
(2)全体排成一排,甲不站在排头也不站在排尾;
(3)全体排成一排,女生必须站在一起;
(4)全体排成一排,男生不能相邻.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com