练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在正方体ABCD-A1B1C1D1中，M，N，Q分别是棱D1C1，A1D1，BC的中点，P在对角线BD1上，且BP=BD1，给出下面四个命题：

    (1)MN∥平面APC；(2)C1Q∥平面APC；(3)A，P，M三点共线；(4)平面MNQ∥平面APC.正确的序号为　(　　)

    A. (1)(2) B. (1)(4) C. (2)(3) D. (3)(4)

    【答案】C

    【解析】(1)MN∥AC，连接AM，CN，易得AM，CN交于点P，即MN平面PAC，所以MN∥平面APC是错误的；(2)平面APC延展，可知M，N在平面APC上，AN∥C1Q，所以C1Q∥平面APC，是正确的；(3)由BP=BD1，以及相似，可得A，P，M三点共线，是正确的；

    (4)直线AP延长到M，则M在平面MNQ内，又在平面APC内，所以平面MNQ∥平面APC，是错误的.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某大学的名同学准备拼车去旅游，其中大一、大二、大三、大四每个年级各两名，分乘甲、乙两辆汽车.每车限坐名同学(乘同一辆车的名同学不考虑位置)，其中大一的孪生姐妹需乘同一辆车，则乘坐甲车的名同学中恰有名同学是来自于同一年级的乘坐方式共有_______种（有数字作答）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中，设BC的中点为M，GH的中点为N.

    (1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由).

    (2)判断平面BEG与平面ACH的位置关系，并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为正整数，数列满足，，设数列满足.

    （1）求证：数列为等比数列；

    （2）若数列是等差数列，求实数的值；

    （3）若数列是等差数列，前项和为，对任意的，均存在，使得成立，求满足条件的所有整数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （Ⅰ）当时，求的最大值；

    （Ⅱ）若对，恒成立，求的取值范围；

    （Ⅲ）证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如：

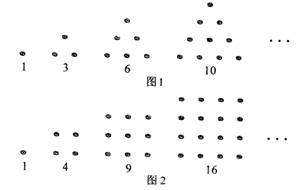
    他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4，9，16，…这样的数为正方形数.下列数中既是三角形数又是正方形数的是（ ）

    A. 36 B. 45 C. 99 D. 100

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列给出的输入语句、输出语句和赋值语句：

    （1）输出语句INPUT ，b，c

    （2）输入语句INPUT =3

    （3）赋值语句3=A

    （4）赋值语句A=B=C

    则其中正确的个数是（ ）

    （A）0 （B）1 （C）2 （D）3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，用符号表示不超过的最大整数，若函数有且仅有3个零点，则的取值范围是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本，已知这40名学生的成绩全部在40分至100分之间，现将成绩按如下方式分成6组，第一组；第二组；…；第六组，并据此绘制了如图所示的频率分布直方图．

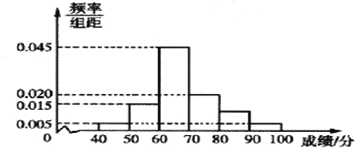
    （1）求成绩在区间内的学生人数；

    （2）从成绩大于等于80分的学生中随机选取2名，求至少有1名学生的成绩在区间内的概率．

    查看答案和解析>>

    同步练习册答案