练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中，设BC的中点为M，GH的中点为N.

    (1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由).

    (2)判断平面BEG与平面ACH的位置关系，并证明你的结论.

    【答案】(1) 见解析(2) 见解析

    【解析】试题分析：(Ⅰ)直接标出点F,G,H的位置.
    (Ⅱ)先证BCHE为平行四边形,可以知道BE∥平面ACH,同理可证BG∥平面ACH,即可证明平面BEG∥平面ACH.

    试题解析：(1)点F，G，H的位置如图所示.

    (2)平面BEG∥平面ACH.证明如下：

    因为ABCD-EFGH为正方体，

    所以BC∥FG，BC=FG，

    又FG∥EH，FG=EH，所以BC∥EH，BC=EH

    于是BCHE为平行四边形.所以BE∥CH，

    又CH平面ACH，BE平面ACH，

    所以BE∥平面ACH.同理BG∥平面ACH，

    又BE∩BG=B，所以平面BEG∥平面ACH.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

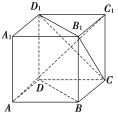
    【题目】【2017唐山模拟】如图，ABCDA1B1C1D1为正方体，连接BD，AC1，B1D1，CD1，B1C，现有以下几个结论：①BD∥平面CB1D1；②AC1⊥平面CB1D1；③AC1与底面ABCD所成角的正切值是；④CB1与BD为异面直线，其中所有正确结论的序号为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 ，函数

    （1）若 在 上单调递增，求 的取值范围；

    （2）记 为 在 上的最大值，求 的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c，向量m＝(cos B，cos C)，n＝(2a＋c，b)，且m⊥n.

    (1)求角B的大小；

    (2)若b＝，求a＋c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过点P(1，2)引直线，使A(2，3)，B(4，-5)到它的距离相等，则这条直线的方程为　(　　)

    A. 4x+y-6=0

    B. x+4y-6=0

    C. 2x+3y-7=0或x+4y-6=0

    D. 3x+2y-7=0或4x+y-6=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)的图像与函数h(x)=的图像关于点Ａ（0，1）对称。

    （１）求函数f(x)的解析式；

    （２）若g(x)＝xf(x)＋ax，且g(x)在区间（0,4］上为减函数，求实数a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

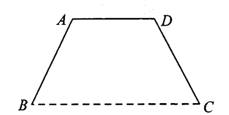
    【题目】某单位将举办庆典活动，要在广场上竖立一形状为等腰梯形的彩门（如图）．设计要求彩门的面积为（单位：），高为（单位：）（为常数）．彩门的下底固定在广场底面上，上底和两腰由不锈钢支架构成，设腰和下底的夹角为，不锈钢支架的长度和记为．

    （1）请将表示成关于的函数；

    （2）问当为何值最小，并求最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体ABCD-A1B1C1D1中，M，N，Q分别是棱D1C1，A1D1，BC的中点，P在对角线BD1上，且BP=BD1，给出下面四个命题：

    (1)MN∥平面APC；(2)C1Q∥平面APC；(3)A，P，M三点共线；(4)平面MNQ∥平面APC.正确的序号为　(　　)

    A. (1)(2) B. (1)(4) C. (2)(3) D. (3)(4)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

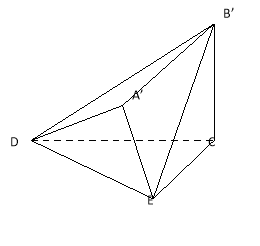
    【题目】已知直角梯形中，是边长为2的等边三角形，．沿将折起，使至处，且；然后再将沿折起，使至处，且面面，和在面的同侧．

    (Ⅰ) 求证：平面；

    (Ⅱ) 求平面与平面所构成的锐二面角的余弦值．

    查看答案和解析>>

    同步练习册答案