Question

【题目】设 ，函数

（1）若 在 上单调递增，求 的取值范围；

（2）记 为 在 上的最大值，求 的最小值．

Answer 1

【答案】（1） 或 ；（2）.

【解析】试题分析：（1）分类讨论当时，当时，当时，运用单调性，判断求解即可；

（2）对时，当，再分时， ， ，运用单调性，求得最大值，再由分段函数的单调性，求得最小值.

试题解析：

（1） 设 为对称轴，

当 时， ，所以 在 上单调递增，

所以 符合题意；

当 时， ，所以 在 上单调递增，

所以 符合题意；

span> 当 时， ，

所以 在 上单调递增，即只需满足 ，即有 ，

所以 符合题意．综上， 或 ．

（2） 若 ， ，对称轴为 ，

在 递增，可得 ；

若 ，则 （）在 递增，在 递减，在 递增，

若 ，即 时， 在 递增，可得 ；

若 ，即 ，可得 的最大值为 ；

若 ，即

，可得 的最大值为 ．

即有 ；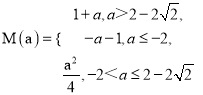

当 时， （）；

当 时， ；

当 ，可得 ．

综上可得 的最小值为 ．