
思路分析:集合A是方程x2-2x-8=0的解集,集合B是关于x的方程x2+ax+a2-12=0的解集,由B![]() A,且B≠
A,且B≠![]() ,按集合B中含有元素的个数分类讨论,分别列出关于a的方程,解方程即可得实数a的值.
,按集合B中含有元素的个数分类讨论,分别列出关于a的方程,解方程即可得实数a的值.
解:由题意,得A={-2,4},集合B是关于x的方程x2+ax+a2-12=0的解集.
∵B![]() A,且B≠
A,且B≠![]() ,∴B={-2}或{4}或{-2,4}.
,∴B={-2}或{4}或{-2,4}.
当集合B中含有一个元素时,则有Δ=a2-4(a2-12)=0,解得a=±4.
若a=4,则B={x∈R|x2+4x+4=0}={-2},则a=4符合题意;
若a=-4,则B={x∈R|x2-4x+4=0}={2},则a=-4不合题意.
当集合B中含有两个元素,即B={-2,4}时,则-2,4是关于x的方程x2+ax+a2-12=0的解.
∴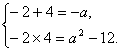 解得a=-2.
解得a=-2.
综上所得,a=4,或a=-2,即实数a的取值集合是{-2,4}.


科目:高中数学 来源:走向清华北大同步导读·高一数学·上 题型:013
已知函数![]() (x∈R且x≠1),那么它的反函数为
(x∈R且x≠1),那么它的反函数为
[ ]
A.![]() (x∈R,且x≠1)
(x∈R,且x≠1)
B.![]() (x∈R,且x≠6)
(x∈R,且x≠6)
C.![]() (x∈R,且x≠
(x∈R,且x≠![]() )
)
D.![]() (x∈R,且x≠-5)
(x∈R,且x≠-5)
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试、理科数学(辽宁卷) 题型:013
已知f(x)与g(x)是定义在R上的连续函数,如果f(x)与g(x)仅当x=0时的函数值为0,且f(x)≥g(x),那么下列情形不可能出现的是
A.0是f(x)的极大值,也是g(x)的极大值
B.0是f(x)的极小值,也是g(x)的极小值
C.0是f(x)的极大值,但不是g(x)的极值
D.0是f(x)的极小值,但不是g(x)的极值
查看答案和解析>>
科目:高中数学 来源:2012高考数学二轮名师精编精析(3):函数性质 题型:013
已知f(x)与g(x)是定义在R上的连续函数,如果f(x)与g(x)仅当x=0时的函数值为0,且f(x)≥g(x),那么下列情形不可能出现的是
0是f(x)的极大值,也是g(x)的极大值
0是f(x)的极小值,也是g(x)的极小值
0是f(x)的极大值,但不是g(x)的极值
0是f(x)的极小值,但不是g(x)的极值
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)已知af(x)+bf(![]() )=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
)=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
(3)f(x)是R上的奇函数,且x∈(-∞,0)时,f(x)=x2+2x,求f(x);
(4)某工厂生产一种机器的固定成本为5 000元,且每生产100部,需要增加投入2 500元,对销售市场进行调查后得知,市场对此产品的需求量为每年500部,已知销售收入的函数为H(x)=500x-![]() x2,其中x是产品售出的数量,且0≤x≤500.若x为年产量,y表示利润,求y=f(x)的解析式.
x2,其中x是产品售出的数量,且0≤x≤500.若x为年产量,y表示利润,求y=f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练15练习卷(解析版) 题型:选择题
已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
(A)?x∈R,f(x)≤f(x0) (B)?x∈R,f(x)≥f(x0)
(C)?x∈R,f(x)≤f(x0) (D)?x∈R,f(x)≥f(x0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com