解:(Ⅰ)函数的定义域为(-1,+∞).(1分)
∵
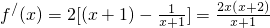
,
由f
/(x)>0,得x>0;由f
/(x)<0,得-1<x<0.(3分)
∴f(x)的递增区间是(0,+∞),递减区间是(-1,0).(4分)
(Ⅱ)∵由
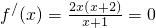
,得x=0,x=-2(舍去)
由(Ⅰ)知f(x)在
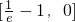
上递减,在[0,e-1]上递增.
高三数学(理科)答案第3页(共6页)
又
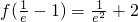
,f(e-1)=e
2-2,且
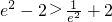
.
∴当
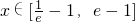
时,f(x)的最大值为e
2-2.
故当m>e
2-2时,不等式f(x)<m恒成立.(9分)
(Ⅲ)方程f(x)=x
2+x+a,x-a+1-2ln(1+x)=0.
记g(x)=x-a+1-2ln(1+x),
∵
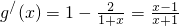
,
由g
/(x)>0,得x>1或x<-1(舍去).由g
/(x)<0,得-1<x<1.
∴g(x)在[0,1]上递减,在[1,2]上递增.
为使方程f(x)=x
2+x+a在区间[0,2]上恰好有两个相异的实根,
只须g(x)=0在[0,1]和(1,2]上各有一个实数根,于是有
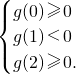
∵2-2ln2<3-2ln3,
∴实数a的取值范围是2-2ln2<a≤3-2ln3.(14分)
分析:(Ⅰ)已知f(x)=(1+x)
2-2ln(1+x)求出函数的导数f′(x),然后令f′(x)=0,解出函数的极值点,最后根据导数判断函数的单调性,从而求解;
(Ⅱ)由题意当
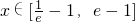
时,不等式f (x)<m恒成立,只要求出f(x)的最大值小于m就可以了,从而求出实数m的取值范围;
(Ⅲ)已知方程f(x)=x
2+x+a在区间[0,2]上恰好有两个相异的实根,整理移项得方程g(x)=x-a+1-2ln(1+x)=0在区间[0,2]上恰好有两个相异的实根,利用函数的增减性得根,于是有
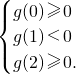
,从而求出实数a的取值范围.
点评:此题主要考查对数函数的导数,函数单调性的判定,函数最值,函数、方程与不等式等基础知识,一般出题者喜欢考查学生的运算求解能力、推理论证能力及分析与解决问题的能力,要出学生会用数形结合的思想、分类与整合思想,化归与转化思想、有限与无限的思想来解决问题.

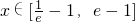 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;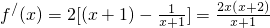 ,
,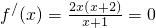 ,得x=0,x=-2(舍去)
,得x=0,x=-2(舍去)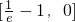 上递减,在[0,e-1]上递增.
上递减,在[0,e-1]上递增.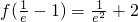 ,f(e-1)=e2-2,且
,f(e-1)=e2-2,且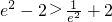 .
.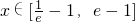 时,f(x)的最大值为e2-2.
时,f(x)的最大值为e2-2.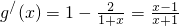 ,
,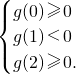
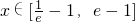 时,不等式f (x)<m恒成立,只要求出f(x)的最大值小于m就可以了,从而求出实数m的取值范围;
时,不等式f (x)<m恒成立,只要求出f(x)的最大值小于m就可以了,从而求出实数m的取值范围;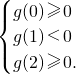 ,从而求出实数a的取值范围.
,从而求出实数a的取值范围.
