分析:解法一:(1):利用勾股定理的逆定理判断出AC⊥BC,同时因为三棱柱为直三棱柱,从而证出.
(2):因为D为AB的中点,连接C
1B和CB
1交点为E,连接DE,∵D是AB的中点,E是BC
1的中点,根据三角形中位线定理得DE∥AC
1,得到AC
1∥平面CDB
1;第三问:因为AC
1∥DE,所以∠CED为AC
1与B
1C所成的角,求出此角即可.
解法二:利用空间向量法.如图建立坐标系,
(1):证得向量点积为零即得垂直.
(2):
=λ
,
与
两个向量或者共线或者平行可得.第三问:
解答: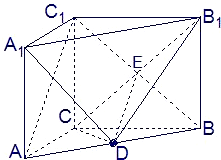
证明:(Ⅰ)直三棱柱ABC-A
1B
1C
1,底面三边长AC=3,BC=4,AB=5,
∴AC⊥BC,且BC
1在平面ABC内的射影为BC,∴AC⊥BC
1;
(Ⅱ)设CB
1与C
1B的交点为E,连接DE,
∵D是AB的中点,E是BC
1的中点,
∴DE∥AC
1,
∵DE?平面CDB
1,AC
1?平面CDB
1,
∴AC
1∥平面CDB
1;
(Ⅲ)∵DE∥AC
1,∴∠CED为AC
1与B
1C所成的角,
在△CED中,ED=
AC
1=
,CD=
AB=
,CE=
CB
1=2
,
∴cos∠CED=
=
,
∴异面直线AC
1与B
1C所成角的余弦值
.
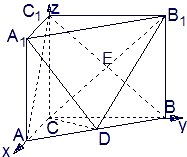
解法二:
∵直三棱锥ABC-A
1B
1C
1底面三边长AC=3,BC=4,AB=5,AC,BC,CC
1两两垂直.
如图建立坐标系,则C(0,0,0),A(3,0,0),C
1(0,0,4),B(0,4,0),B
1(0,4,4),D(
,2,0)(Ⅰ)∵
=(-3,0,0),
=(0,4,4),
∴
•
=0,
∴
⊥
.
(Ⅱ)设CB
1与C
1B的交点为E,则E(0,2,2)
∵
=(-
,0,2),
=(-3,0,4),
∴
=
,∴
∥
∵DE?平面CDB
1,AC
1?平面CDB
1,∴AC
1∥平面CDB
1.
(Ⅲ)∵
=(-3,0,0),
=(0,4,4),
∴cos<
,
>=
=
,
∴异面直线AC
1与B
1C所成角的余弦值为
.
点评:本题考查向量的几何意义a•b=|a||b|cosα;向量垂直?a•b=0;直线与平面的证明方法.

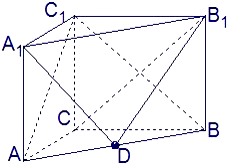 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D为AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D为AB的中点. 证明:(Ⅰ)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
证明:(Ⅰ)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,


 阅读快车系列答案
阅读快车系列答案



