
【题目】某蛋糕店制作并销售一款蛋糕,制作一个蛋糕成本3元,且以8元的价格出售,若当天卖不完,剩下的则无偿捐献给饲料加工厂。根据以往100天的资料统计,得到如下需求量表。该蛋糕店一天制作了这款蛋糕![]() 个,以
个,以![]() (单位:个,
(单位:个,![]() ,
,![]() )表示当天的市场需求量,
)表示当天的市场需求量,![]() (单位:元)表示当天出售这款蛋糕获得的利润.
(单位:元)表示当天出售这款蛋糕获得的利润.
需求量/个 |
|
|
|
|
|
天数 | 15 | 25 | 30 | 20 | 10 |
(1)当![]() 时,若
时,若![]() 时获得的利润为
时获得的利润为![]() ,
,![]() 时获得的利润为
时获得的利润为![]() ,试比较
,试比较![]() 和
和![]() 的大小;
的大小;
(2)当![]() 时,根据上表,从利润
时,根据上表,从利润![]() 不少于570元的天数中,按需求量分层抽样抽取6天.
不少于570元的天数中,按需求量分层抽样抽取6天.
(i)求此时利润![]() 关于市场需求量
关于市场需求量![]() 的函数解析式,并求这6天中利润为650元的天数;
的函数解析式,并求这6天中利润为650元的天数;
(ii)再从这6天中抽取3天做进一步分析,设这3天中利润为650元的天数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,交圆
轴不重合,交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,试问在椭圆
点,试问在椭圆![]() 上是否存在一定点
上是否存在一定点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列(其中
成等差数列(其中![]() ,
,![]() ,
,![]() 分别指直线
分别指直线![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(卷号)2040818101747712
(题号)2050752239689728
(题文)
在平面直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知直线![]() 的参数方程为
的参数方程为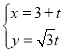 (
(![]() 为参数),曲线C的极坐标方程为
为参数),曲线C的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() =2cos(ωx
=2cos(ωx![]() )(ω>0)满足:f(
)(ω>0)满足:f(![]() )=f(
)=f(![]() ),且在区间(
),且在区间(![]() ,
,![]() )内有最大值但没有最小值,给出下列四个命题:P1:
)内有最大值但没有最小值,给出下列四个命题:P1:![]() 在[0,2π]上单调递减;P2:
在[0,2π]上单调递减;P2:![]() 的最小正周期是4π;P3:
的最小正周期是4π;P3:![]() 的图象关于直线x
的图象关于直线x![]() 对称;P4:
对称;P4:![]() 的图象关于点(
的图象关于点(![]() ,0)对称.其中的真命题是( )
,0)对称.其中的真命题是( )
A.P1,P2B.P2,P4C.P1,P3D.P3,P4
查看答案和解析>>
科目:高中数学 来源: 题型:
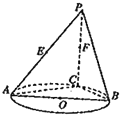
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织高一、高二年级学生进行了“纪念建国70周年”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图和高二年级成绩的频数分布表.
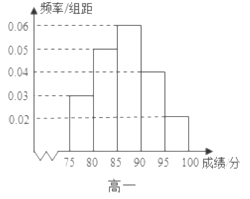
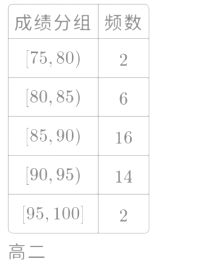
(Ⅰ)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(Ⅱ)在抽取的学生中,从成绩为[95,100]的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率;
(Ⅲ)记高一、高二两个年级知识竞赛的平均分分别为![]() ,试估计
,试估计![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为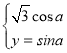 ,(a为参数)。以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
,(a为参数)。以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]() ,将C2逆时针旋转
,将C2逆时针旋转![]() 以后得到曲线C3.
以后得到曲线C3.
(1)写出C1与C3的极坐标方程;
(2)设C2与C3分别交曲线C1于A、B和C、D四点,求四边形ACBD面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点为
,左、右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 关于原点对称,直线
关于原点对称,直线![]() 的斜率的乘积为
的斜率的乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() ,判断直线
,判断直线![]() 的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com