
科目:高中数学 来源:2010年高考试题分项版理科数学之专题十七 选修系列 题型:填空题
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题平分)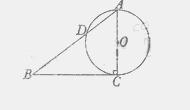
A.(不等式选做题)不等式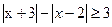 的解集为
的解集为
B. (几何证明选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则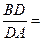
C, (坐标系与参数方程选做题)已知圆C的参数方程为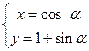 (a为参数)以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
(a为参数)以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为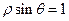 ,则直线l与圆C的交点的直角坐标系为____
,则直线l与圆C的交点的直角坐标系为____
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高考猜押题卷文科数学(一)解析版 题型:填空题
选做题(14、15题,考生只能从中选做一题)
(几何证明选讲选做题)如图4,△ABC中,D、E分别在边AB、AC上,CD平分∠ACB,DE∥BC,如果AC=10,AE=4,那么BC=___________.

查看答案和解析>>
科目:高中数学 来源:2010-2011年广东省汕头市高二下学期期末考试文科数学 题型:填空题
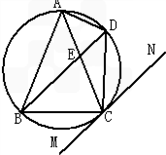
(几何证明选讲选做题)如图所示, 圆的内接△ABC的∠C的平分线CD延长后交圆于点E, 连接BE,已知BD=3,CE=7,BC=5,则线段BE= .
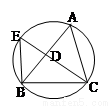
查看答案和解析>>
科目:高中数学 来源:2011届广东省高考猜押题卷文科数学(一)解析版 题型:填空题
选做题(14、15题,考生只能从中选做一题)
(几何证明选讲选做题)如图4,△ABC中,D、E分别在边AB、AC上,CD平分∠ACB,DE∥BC,如果AC=10,AE=4,那么BC=___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com