
(1)试用t表示切线PQ的方程;
(2)试用t表示△QAP的面积g(t),若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)若S△QAP∈[![]() ,64],试求出点P横坐标的取值范围.
,64],试求出点P横坐标的取值范围.
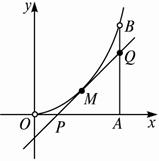
解析:(1)设点M(t,t2),?
又f′(x)=2x,?
∴过点M的切线PQ的斜率k=2t.?
∴切线PQ的方程为y=2tx-t2.?
(2)由(1)可求得P(![]() ,0),Q(6,12t-t2),?
,0),Q(6,12t-t2),?
∴g(t)=S△QAP=![]() (6-
(6-![]() t)(12t-t2)=
t)(12t-t2)=![]() -6t2+36t(0<t<6).?
-6t2+36t(0<t<6).?
由于g′(t)=![]() t2-12t+36,?
t2-12t+36,?
令g′(t)<0,得4<t<12,∴4<t<6.?
∴函数g(t)的单调递减区间是(4,6),因此m的最小值为4.?
(3)由(2)知函数g(t)在(4,6)上递减,??
∴此时S△QAP∈(g(6),g(4))=(54,64).??
∴g(t)的值域为(0,64).?
由S△QAP∈[![]() ,64],可得1≤t<6.?
,64],可得1≤t<6.?
∴![]() ≤
≤![]() <3,即点P的横坐标的取值范围是[
<3,即点P的横坐标的取值范围是[![]() ,3).
,3).


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:高中数学 来源: 题型:
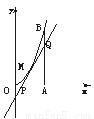
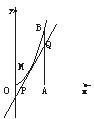 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,查看答案和解析>>
科目:高中数学 来源: 题型:
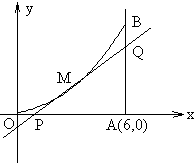 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,查看答案和解析>>
科目:高中数学 来源: 题型:
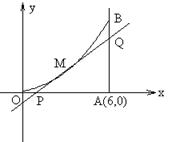
如图所示,曲线段OMB是函数f(x)=x2(0<x<6=的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,⑴试用t表示切线PQ的方程;⑵试用t表示出△QAP的面积g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;⑶若S△QAP∈[![]() ],试求出点P横坐标的取值范围
],试求出点P横坐标的取值范围
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:14.5 导数的综合问题(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com