
(本题满分10分) 如图,已知 平面
平面 ,
, 于D,
于D, 。
。

(Ⅰ)令 ,
, ,试把
,试把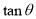 表示为
表示为 的函数,并求其最大值;
的函数,并求其最大值;
(Ⅱ)在直线PA上是否存在一点Q,使得 ?
?
(Ⅰ)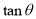 =
=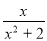 ,
,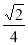 ;(Ⅱ)存在.
;(Ⅱ)存在.
【解析】
试题分析:(Ⅰ)利用三角形的一个外角等于其不相邻的两内角和,所以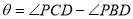 ,再根据
,再根据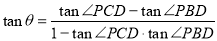 即可求出;根据
即可求出;根据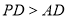 来确定自变量
来确定自变量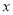 的范围,进而确定
的范围,进而确定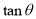 的最大值;(Ⅱ)点Q的存在性等价于:是否存在点Q使得
的最大值;(Ⅱ)点Q的存在性等价于:是否存在点Q使得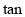
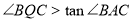 ,得出关于
,得出关于 的不等式,若不等式有解,则存在这样的点,否则就不存在这样的点.
的不等式,若不等式有解,则存在这样的点,否则就不存在这样的点.
试题解析:(Ⅰ)∵  面
面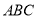 ,
,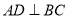 于D,
于D,
∴  。
。
∴  。
。
∴ 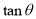
 。
。
∵  为
为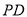 在面
在面 上的射影。
上的射影。
∴  ,即
,即 。
。
∴ 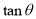
 。
。
即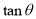 的最大值为
的最大值为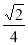 ,等号当且仅当
,等号当且仅当 时取得.
时取得.
(Ⅱ)由正切函数的单调性可知:点Q的存在性等价于:是否存在点Q使得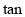
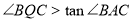 。
。
 。
。
令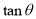
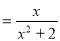
 ,解得:
,解得: ,与
,与 的交集非空.
的交集非空.
∴ 满足条件的点Q存在。
考点:1、两角差的正切公式;2、空间想象能力、综合分析和解决问题的能力。


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:2014-2015学年浙江省实验班高二10月月考理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(Ⅰ)求函数 在
在 上的最小值;
上的最小值;
(Ⅱ)若存在 使不等式
使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高二10月月考数学试卷(解析版) 题型:解答题
(本小题10分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB=2,M, N分别为PA, BC的中点.

(Ⅰ)证明:MN∥平面PCD;
(Ⅱ)求MN与平面PAC所成角的正切值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高二10月月考数学试卷(解析版) 题型:选择题
如图正三棱柱 的底面边长为
的底面边长为 ,高为2,
,高为2,
一只蚂蚁要从顶点 沿三棱柱的表面爬到顶点
沿三棱柱的表面爬到顶点 ,若侧面
,若侧面
 紧贴墙面(不能通行),则爬行的最短路程是( )
紧贴墙面(不能通行),则爬行的最短路程是( )
A. B.
B. C. 4 D.
C. 4 D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高二10月月考数学试卷(解析版) 题型:选择题
已知正方体的棱长为1,则它的内切球与外接球半径的比值为( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省嘉兴市高二上学期第一次阶段测试数学试卷(解析版) 题型:填空题
有两个相同的直三棱柱,高为 ,底面三角形的三边长分别为
,底面三角形的三边长分别为 。用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则
。用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则 的取值范围是_________
的取值范围是_________
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南郑州外国语学校高二上学期第一次月考文科数学卷(解析版) 题型:解答题
(本小题满分12分)已知 ,不等式
,不等式 的解集是
的解集是 ,
,
(1)求 的解析式;
的解析式;
(2)若对于任意 ,不等式
,不等式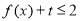 恒成立,求
恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com