
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
|
房屋面积(m2) |
115 |
110 |
80 |
135 |
105 |
|
销售价格(万元) |
24.8 |
21.6 |
18.4 |
29.2 |
22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)根据(2)的结果估计当房屋面积为150 m2时的销售价格.
(1)数据对应的散点图如图所示.
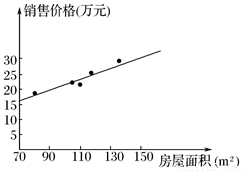
(2)所求回归直线方程为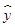 =0.1962x+1.8166.
=0.1962x+1.8166.
(3)销售价格的估计值为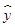 =0.1962×150+1.8166=31.2466(万元).
=0.1962×150+1.8166=31.2466(万元).
【解析】
试题分析:(1)数据对应的散点图如图所示.
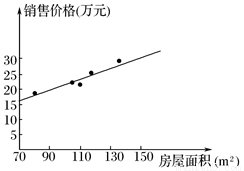
(2) =109,
=109,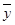 =23.2,
=23.2,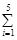 (xi-
(xi- )2=1570,
)2=1570,
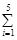 (xi-
(xi- )(yi-
)(yi-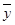 )=308,
)=308,
设所求的回归直线方程为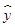 =bx+a,
=bx+a,
则b=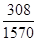 ≈0.1962,
≈0.1962,
a=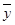 -b
-b =23.2-109×
=23.2-109×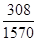 ≈1.8166,
≈1.8166,
故所求回归直线方程为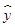 =0.1962x+1.8166.
=0.1962x+1.8166.
(3)据(2),当x=150 m2时,销售价格的估计值为
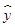 =0.1962×150+1.8166=31.2466(万元).
=0.1962×150+1.8166=31.2466(万元).
考点:回归直线方程
点评:中档题,确定回归直线方程,关键是准确计算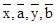 等相关元素,对计算能力要求较高。高考题中,常常以填空题形式出现。
等相关元素,对计算能力要求较高。高考题中,常常以填空题形式出现。


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
| ? |
| b |
| |||||||
|
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 房屋面积m2 | 110 | 90 | 80 | 100 | 120 |
| 销售价格(万元) | 33 | 31 | 28 | 34 | 39 |
| ? |
| b |
| |||||||
|
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 80 | 90 | 100 | 110 | 120 |
| y | 48 | 52 | 63 | 72 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:
房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为150 m2时的销售价格.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com