
设等差数列{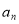 }的前n项和为Sn,且S4=4S2,
}的前n项和为Sn,且S4=4S2,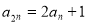 .
.
(1)求数列{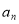 }的通项公式;
}的通项公式;
(2)设数列{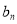 }满足
}满足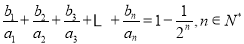 ,求{
,求{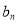 }的前n项和Tn;
}的前n项和Tn;
(3)是否存在实数K,使得Tn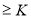 恒成立.若有,求出K的最大值,若没有,说明理由.
恒成立.若有,求出K的最大值,若没有,说明理由.
(1)an=2n﹣1,n∈N*;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)由于{an}是等差数列,故只需求出其首项a1和公差d即可得其通项公式.由S4=4S2,a2n=2an+1得方程组: ,这个方程组中,看起来有3个未知数,但n抵消了(如果n不能抵消,则左右两边对应系数相等),故实质上只有两个未知数.解这个方程组即可(也可以取n=2).(2)首先求出{bn}的通项公式. 已知
,这个方程组中,看起来有3个未知数,但n抵消了(如果n不能抵消,则左右两边对应系数相等),故实质上只有两个未知数.解这个方程组即可(也可以取n=2).(2)首先求出{bn}的通项公式. 已知 求
求 ,则
,则 .在本题中,由已知
.在本题中,由已知 可得:当n≥2时,
可得:当n≥2时, ,显然,n=1时符合.由(1)得,an=2n﹣1,n∈N*.从而
,显然,n=1时符合.由(1)得,an=2n﹣1,n∈N*.从而 ,n∈N*.这个数列用错位相消法便可求得其和
,n∈N*.这个数列用错位相消法便可求得其和 .(3)Tn
.(3)Tn 恒成立,则
恒成立,则 .为了求
.为了求 ,需要研究
,需要研究 的单调性,为了研究
的单调性,为了研究 的单调性,需考查
的单调性,需考查 的符号.
的符号.
试题解析:(1)设等差数列{an}的首项为a1,公差为d,由S4=4S2,a2n=2an+1得: ,
,
解得a1=1,d=2.
∴an=2n﹣1,n∈N*.(2)由已知 ,得:
,得:
当n=1时, ,
,
当n≥2时, ,显然,n=1时符合.
,显然,n=1时符合.
∴ ,n∈N*,由(1)知,an=2n﹣1,n∈N*.∴
,n∈N*,由(1)知,an=2n﹣1,n∈N*.∴ ,n∈N*.
,n∈N*.
又 ,∴
,∴ ,
,
两式相减得:
所以 .
.
(3) ,
,
所以 单调递增,
单调递增,
所以 ,
,
所以 .
.
考点:1、等差数列与等比数列;2、数列的和;3、数列与不等式.


科目:高中数学 来源:2013-2014学年天津市河东区高三一模理科数学试卷(解析版) 题型:解答题
给定椭圆 .称圆心在原点O,半径为
.称圆心在原点O,半径为 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线 ,使得
,使得 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断 是否垂直?并说明理由.
是否垂直?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市南开区高三第一次模拟考试理科数学试卷(解析版) 题型:填空题
如图,平行四边形ABCD的两条对角线相交于点M,点P是MD的中点.若 =2,
=2, =1,且
=1,且 BAD=60o,则
BAD=60o,则  。
。

查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市南开区高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
已知实数x,y满足约束条件 ,则
,则 的最小值是( ).
的最小值是( ).
(A)5 (B)-6 (C)10 (D)-l0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考理科数学试卷(解析版) 题型:填空题
某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 (用数字作答).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考理科数学试卷(解析版) 题型:选择题
已知向量a=(sin θ,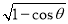 ),b=(1,
),b=(1,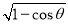 ),其中θ∈
),其中θ∈ ,则一定有 ( )
,则一定有 ( )
A.a∥b B.a⊥b C.a与b的夹角为45° D.|a|=|b|
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考文科数学试卷(解析版) 题型:选择题
过椭圆的一个焦点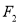 作垂直于实轴的弦
作垂直于实轴的弦 ,
, 是另一焦点,若∠
是另一焦点,若∠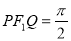 ,则椭圆的离心率
,则椭圆的离心率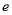 等于( )
等于( )
A.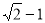 B.
B.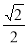 C.
C.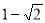 D.
D.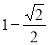
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试文科数学试卷(解析版) 题型:选择题
已知函数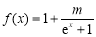 ,若
,若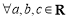 ,
,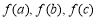 为某一个三角形的边长,则实数m的取值范围是( )
为某一个三角形的边长,则实数m的取值范围是( )
(A)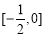 (B)
(B)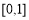 (C)
(C)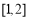 (D)
(D)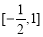
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com