
| 女生 | 男生 | 总计 | |
| 爱吃零食 | |||
| 不爱吃零食 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
分析 根据列联表运用公式K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d,求出k值,根据计算出的临界值,同临界值表进行比较,即可得出结论.
解答 解:将2×2列联表补充完整:
| 女生 | 男生 | 总计 | |
| 爱吃零食 | 60 | 80 | 140 |
| 不爱吃零食 | 20 | 40 | 60 |
| 总计 | 80 | 120 | 200 |
点评 本题考查了独立性检验的应用,利用临界值的大小可以决定是否拒绝原来的统计假设,属于基础题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一次摸出的是白球与第一次摸出的是黑球 | |
| B. | 摸出后不放回,第一次摸出的是白球,第二次摸出的是黑球 | |
| C. | 摸出后放回,第一次摸出的是白球,第二次摸出的是黑球 | |
| D. | 一次摸两个球,共摸两次,第一次摸出颜色相同的球与第一次摸出颜色不同的球 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | (-3,1) | C. | [-1,3] | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
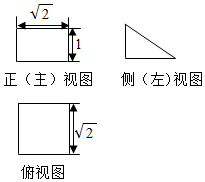 若某空间几何体的三视图如图所示,则该几何体的表面积是( )
若某空间几何体的三视图如图所示,则该几何体的表面积是( )| A. | 1+$\sqrt{2}$+2$\sqrt{3}$ | B. | $\sqrt{2}$+2$\sqrt{3}$+$\sqrt{6}$ | C. | 2+$\sqrt{6}$+$\sqrt{10}$ | D. | 2+2$\sqrt{2}$+$\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com